spkit.entropy_approx

spkit.entropy_approx(x, m, r)

Approximate Entropy \(ApproxEn(X)\) or \(H_{ae}(X)\)

Approximate entropy is more suited for temporal source, (non-IID), such as physiological signals, or signals in general. Approximate entropy like Sample Entropy ( entropy_sample) measures the complexity of a signal by extracting the pattern of m-symbols. m is also called as embedding dimension. r is the tolarance here, which determines the two patterns to be same if their maximum absolute difference is than r.

Parameters:
X1d-array

as signal

mint
embedding dimension, usual value is m=3, however, it depends on the signal.

If signal has high sampling rate, which means a very smooth signal, then any consequitive 3 samples will be quit similar.

rtolarance

usual value is r = 0.2*std(x)

Returns:
ApproxEnfloat

  • approximate entropy value

See also

entropy

Entropy

entropy_sample

Sample Entropy

dispersion_entropy

Dispersion Entropy

entropy_spectral

Spectral Entropy

entropy_svd

SVD Entropy

entropy_permutation

Permutation Entropy

entropy_differential

Differential Entropy

References

Examples

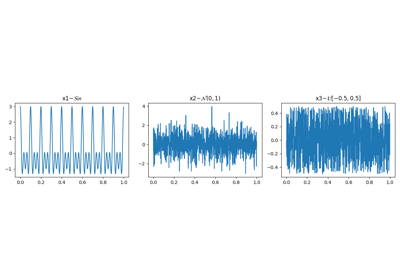
>>> import numpy as np
>>> import spkit as sp
>>> t = np.linspace(0,2,200)
>>> x1 = np.sin(2*np.pi*1*t) + 0.1*np.random.randn(len(t))  # less noisy
>>> x2 = np.sin(2*np.pi*1*t) + 0.5*np.random.randn(len(t))  # very noisy
>>> #Approximate Entropy
>>> H_x1 = sp.entropy_approx(x1,m=3,r=0.2*np.std(x1))
>>> H_x2 = sp.entropy_approx(x2,m=3,r=0.2*np.std(x2))
>>> print('Approximate entropy')
>>> print('Entropy of x1: ApproxEn(x1)= ',H_x1)
>>> print('Entropy of x2: ApproxEn(x2)= ',H_x2)
Approximate entropy
Entropy of x1: ApproxEn(x1)=  0.5661144425748899
Entropy of x2: ApproxEn(x2)=  0.20696275451476875

Examples using spkit.entropy_approx

Sample and Approximate Entropy: Comparison

Sample and Approximate Entropy: Comparison