spkit.dft_analysis

spkit.dft_analysis(x, window='blackmanharris', N=None, scaling_dB=True, normalize_win=True, plot=False, fs=None)

Discrete Fourier Transform: Analysis (DFT)

Analysis of a signal x using the Discrete Fourier Transform

Parameters:
x: 1d-array,

  • input signal ofshape (n,)

window: window-type, default = ‘blackmanharris’

  • if None, rectangular window is used

Nint, default =None

  • FFT size, should be >= len(x) and power of 2

  • if None then N = 2**np.ceil(np.log2(len(n)))

scaling_dB: bool, default True

  • if false, then linear scale of spectrum is returned, else in dB

normalize_win: bool (default True),

  • if to normalize wondow (recommended)

plot: int, (default: 0) for no plot

: 1 for plotting magnitude and phse spectrum : 2 for ploting signal along with spectrum

fsint, deafult=None

  • sampling frequency, only used to plot the signal when plot=2

  • if not provided, fs=1 is used

  • it does not affect any computations

Returns:
mX: magnitude spectrum (of shape=int((N/2)+1)) # positive spectra
pX: phase spectrum same shape as mX
NN-point FFT used for computation

See also

dft_synthesis

Inverse Discreet Fourier Transform - iDFT

stft_analysis

Short-Time Fourier Transform - STFT

stft_synthesis

Inverse Short-Time Fourier Transform - iSTFT

frft

Fractional Frourier Transform - FRFT

ifrft

Inverse Fractional Frourier Transform - iFRFT

sineModel_analysis

Sinasodal Model Decomposition

sineModel_synthesis

Sinasodal Model Synthesis

Notes

#TODO

References

Examples

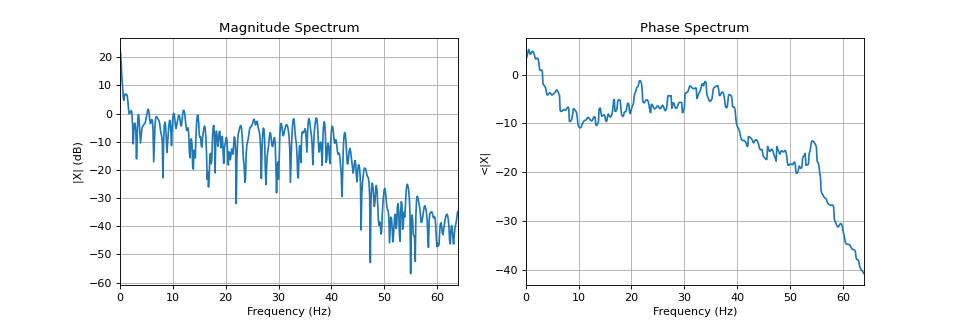
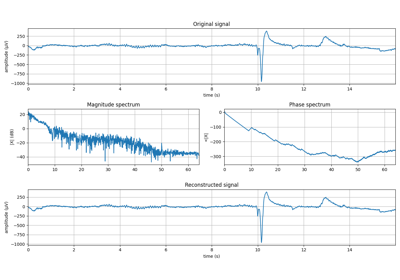
#sp.dft_analysis
import numpy as np
import matplotlib.pyplot as plt
import spkit as sp
x,fs = sp.data.eeg_sample_1ch(ch=1)
x = x[:int(fs*5)]
t = np.arange(len(x))/fs
mX, pX, N = sp.dft_analysis(x,plot=True,fs=fs)
../../_images/spkit-dft_analysis-1.png

Examples using spkit.dft_analysis

Analysis and Synthesis Models

Analysis and Synthesis Models