spkit.ifrft¶
- spkit.ifrft(x, alpha=0.1, method=1, verbose=0)¶
Inverse Fractional Fourier Transform
Inverse Fractional Fourier Transform
- Parameters:
- x: complex-signal
- alpha: scalar, 0<a<4
- method=1, other methods to be implemented
- Returns:
- y: complex signal
- reconstruction using IFRFT
- imaginary part is mostly zero
See also
Notes
# Recostruction of the signal is has some artifact to be removed.
References
wikipedia
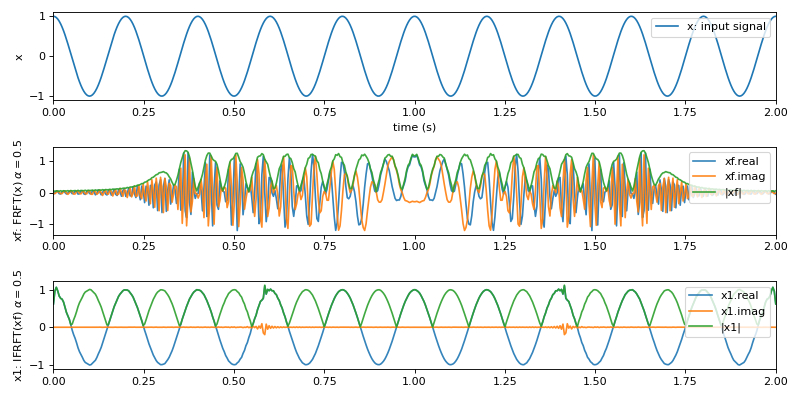
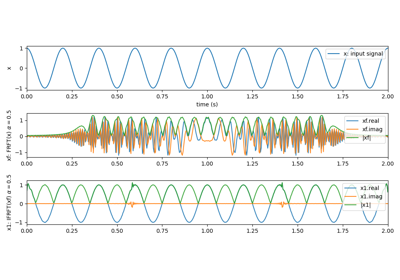
Examples
#sp.ifrft import numpy as np import matplotlib.pyplot as plt import spkit as sp t = np.linspace(0,2,500) x = np.cos(2*np.pi*5*t) xf = sp.frft(x,alpha=0.5) x1 = sp.ifrft(xf,alpha=0.5) plt.figure(figsize=(10,5)) plt.subplot(311) plt.plot(t,x,label='x: input signal') plt.xlim([t[0],t[-1]]) plt.xlabel('time (s)') plt.ylabel('x') plt.legend(loc='upper right') plt.subplot(312) plt.plot(t,xf.real,label='xf.real',alpha=0.9) plt.plot(t,xf.imag,label='xf.imag',alpha=0.9) plt.plot(t,np.abs(xf),label='|xf|',alpha=0.9) plt.xlim([t[0],t[-1]]) plt.ylabel(r'xf: FRFT(x) $\alpha=0.5$') plt.legend(loc='upper right') plt.subplot(313) plt.plot(t,x1.real,label='x1.real',alpha=0.9) plt.plot(t,x1.imag,label='x1.imag',alpha=0.9) plt.plot(t,np.abs(x1),label='|x1|',alpha=0.9) plt.xlim([t[0],t[-1]]) plt.ylabel(r'x1: IFRFT(xf) $\alpha=0.5$') plt.legend(loc='upper right') plt.tight_layout() plt.show()