Note

Go to the end to download the full example code or to run this example in your browser via JupyterLite or Binder

Analysis and Synthesis Models¶

Analysis and Synthesis Models

In this script, we demonstrate following four models:

1 DFT Model
2 STFT Model
3 Fractional Fourier Transform: FRFT
4 Sinasodual Model: Audio

import numpy as np
import matplotlib.pyplot as plt
import spkit as sp
print('spkit version :', sp.__version__)

spkit version : 0.0.9.7

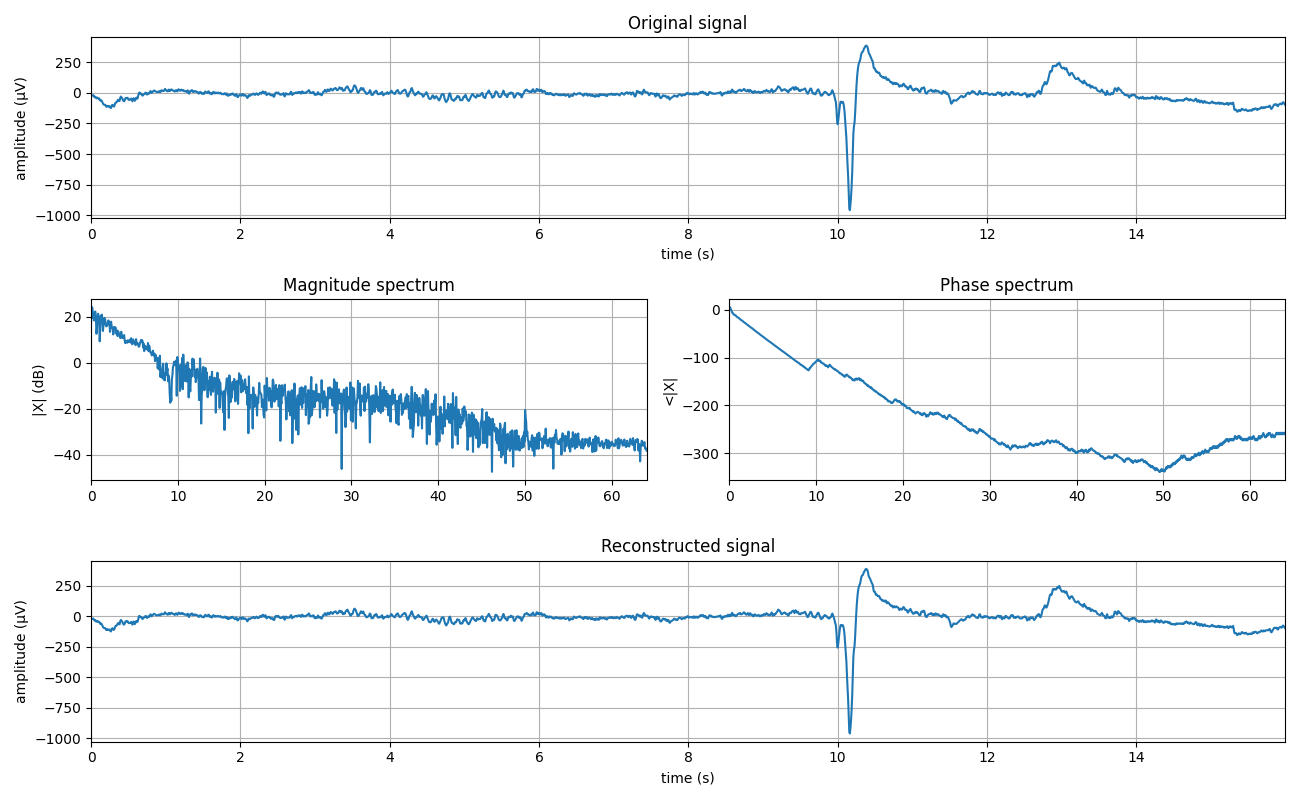
1 DFT Model¶

X,fs, ch_names = sp.data.eeg_sample_14ch()

x = X[:,1]
t = np.arange(len(x))/fs
print(x.shape)


# Analysis

mX, pX, N = sp.dft_analysis(x, window='boxcar')
print(mX.shape,pX.shape, N)


# Synthesis

y = sp.dft_synthesis(mX, pX, M=N, window='boxcar')
print(y.shape)


# plots

plt.figure(figsize=(13,8))
plt.subplot(311)
plt.plot(t,x)
plt.xlim([t[0],t[-1]])
plt.grid()
plt.xlabel('time (s)')
plt.title('Original signal')
plt.ylabel('amplitude (μV)')

plt.subplot(323)
fr = (fs/2)*np.arange(len(mX))/(len(mX)-1)
plt.plot(fr,mX)
plt.xlim([fr[0],fr[-1]])
plt.grid()
plt.ylabel('|X| (dB)')
plt.title('Magnitude spectrum')
plt.subplot(324)
plt.plot(fr,pX)
plt.xlim([fr[0],fr[-1]])
plt.grid()
plt.ylabel('<|X|')
plt.title('Phase spectrum')

plt.subplot(313)
plt.plot(t,y)
plt.xlim([t[0],t[-1]])
plt.grid()
plt.title('Reconstructed signal')
plt.xlabel('time (s)')
plt.ylabel('amplitude (μV)')
plt.tight_layout()
plt.show()


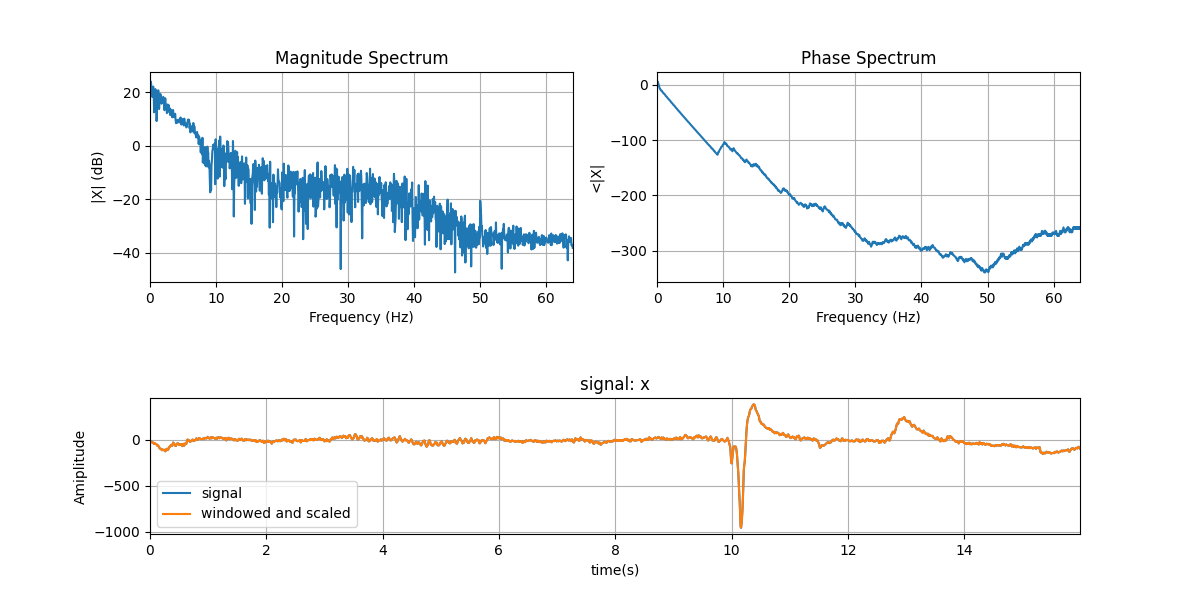
mX, pX, N = sp.dft_analysis(x, window='boxcar',plot=2, fs=fs)


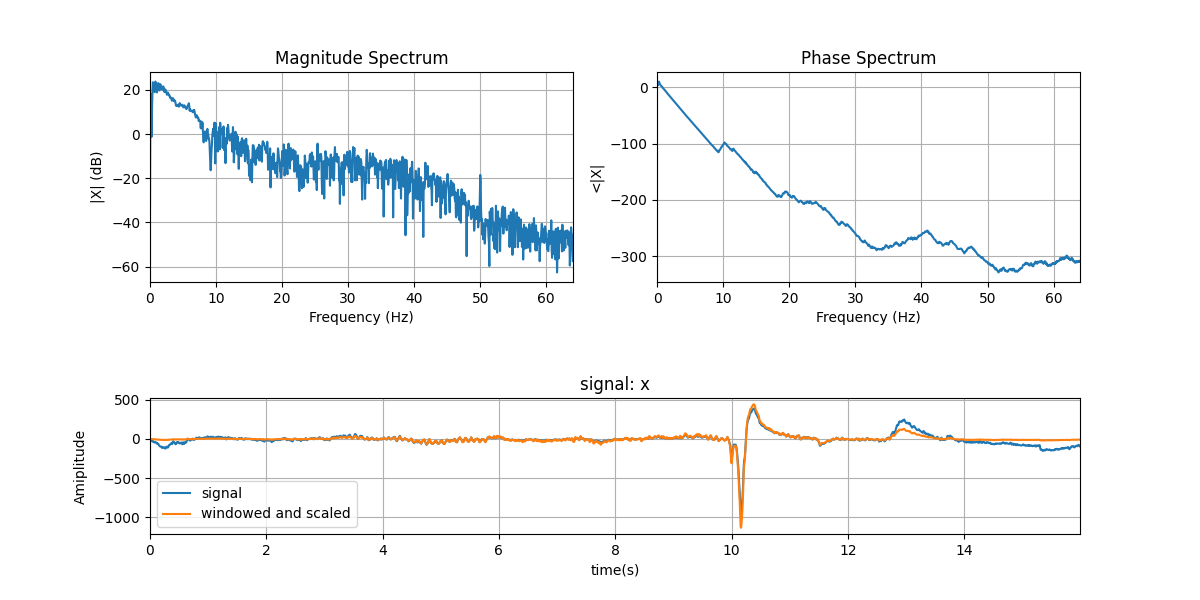
# windowing effect

mX, pX, N = sp.dft_analysis(x, window='hamm',plot=2, fs=fs)

(2048,)
(1025,) (1025,) 2048
(2048,)

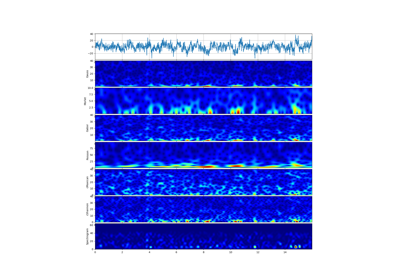
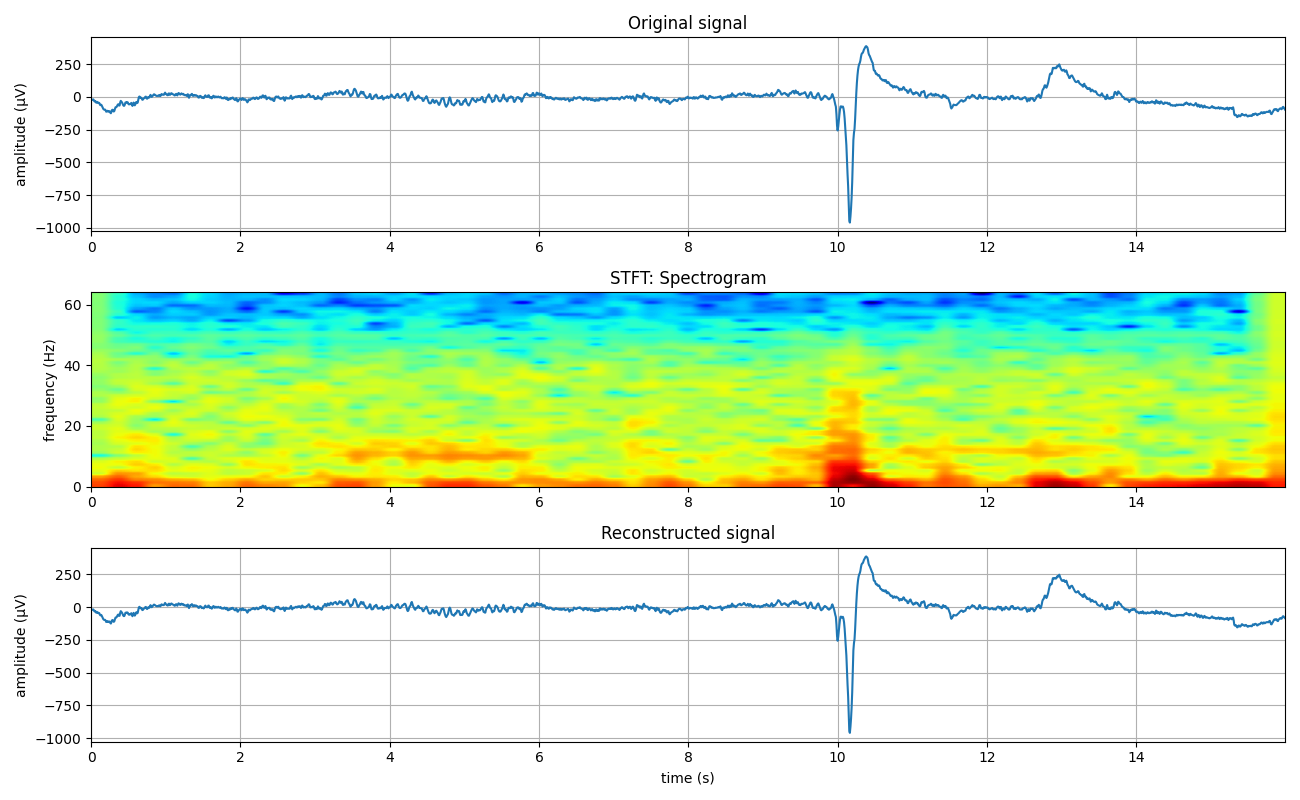
2 STFT Model¶

X,fs, ch_names = sp.data.eeg_sample_14ch()
x = X[:,1]
t = np.arange(len(x))/fs
print(x.shape)


# Analysis: STFT


mXt,pXt = sp.stft_analysis(x, winlen=128, overlap=32,window='blackmanharris',nfft=None)
print(mXt.shape, pXt.shape)


#  Synthesis: Inverse STFT

y = sp.stft_synthesis(mXt, pXt, winlen=128, overlap=32)
print(y.shape)


#  plots


plt.figure(figsize=(13,8))
plt.subplot(311)
plt.plot(t,x)
plt.xlim([t[0],t[-1]])
plt.grid()
plt.title('Original signal')
plt.ylabel('amplitude (μV)')

plt.subplot(312)
plt.imshow(mXt.T,aspect='auto',origin='lower',cmap='jet',extent=[t[0],t[-1],0,fs/2])
plt.title('STFT: Spectrogram')
plt.ylabel('frequency (Hz)')

plt.subplot(313)
plt.plot(t,y[:len(t)])
plt.xlim([t[0],t[-1]])
plt.grid()
plt.title('Reconstructed signal')
plt.xlabel('time (s)')
plt.ylabel('amplitude (μV)')
plt.tight_layout()
plt.show()

Original signal, STFT: Spectrogram, Reconstructed signal

(2048,)
(65, 65) (65, 65)
(2080,)

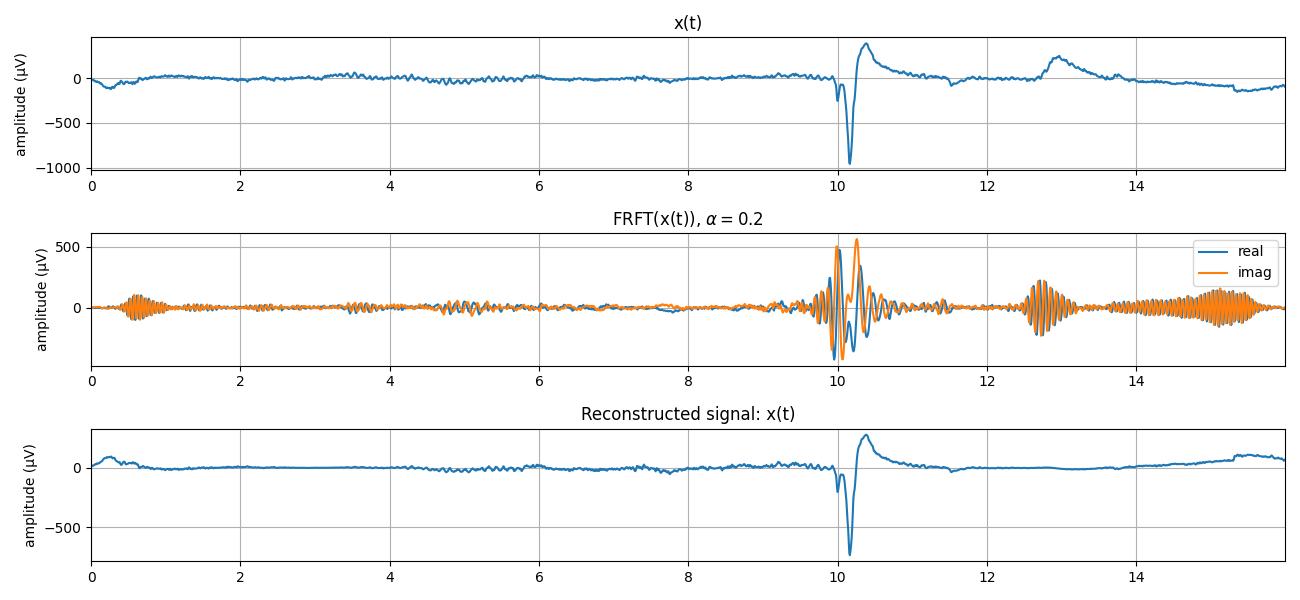
3 Fractional Fourier Transform: FRFT¶

X,fs, ch_names = sp.data.eeg_sample_14ch()

x = X[:,1]
t = np.arange(len(x))/fs
print(x.shape)


#  Analysis

Xa = sp.frft(x.copy(),alpha=0.2)
print(Xa.shape)


# Synthesis

y = sp.ifrft(Xa.copy(),alpha=0.2)
yi = sp.frft(Xa.copy(),alpha=-0.2)
y.shape

# plots

plt.figure(figsize=(13,6))
plt.subplot(311)
plt.plot(t,x)
plt.xlim([t[0],t[-1]])
plt.grid()
plt.title('x(t)')
#plt.xlabel('time (s)')
plt.ylabel('amplitude (μV)')

plt.subplot(312)
plt.plot(t,Xa.real,label='real')
plt.plot(t,Xa.imag,label='imag')
plt.xlim([t[0],t[-1]])
plt.grid()
plt.title(r'FRFT(x(t)), $\alpha=0.2$')
#plt.xlabel('time (s)')
plt.ylabel('amplitude (μV)')
plt.legend()


plt.subplot(313)
plt.plot(t,y.real)
plt.xlim([t[0],t[-1]])
plt.grid()
plt.title('Reconstructed signal: x(t)')
#plt.xlabel('time (s)')
plt.ylabel('amplitude (μV)')
plt.tight_layout()
plt.show()

$x(t), FRFT(x(t)), $\alpha=0.2$, Reconstructed signal: x(t)$

(2048,)
(2048,)

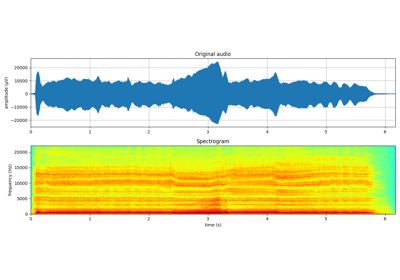
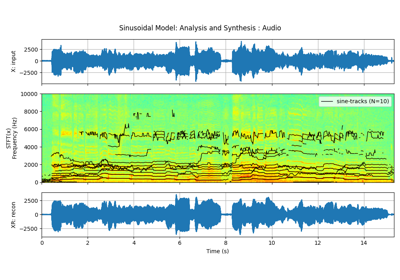
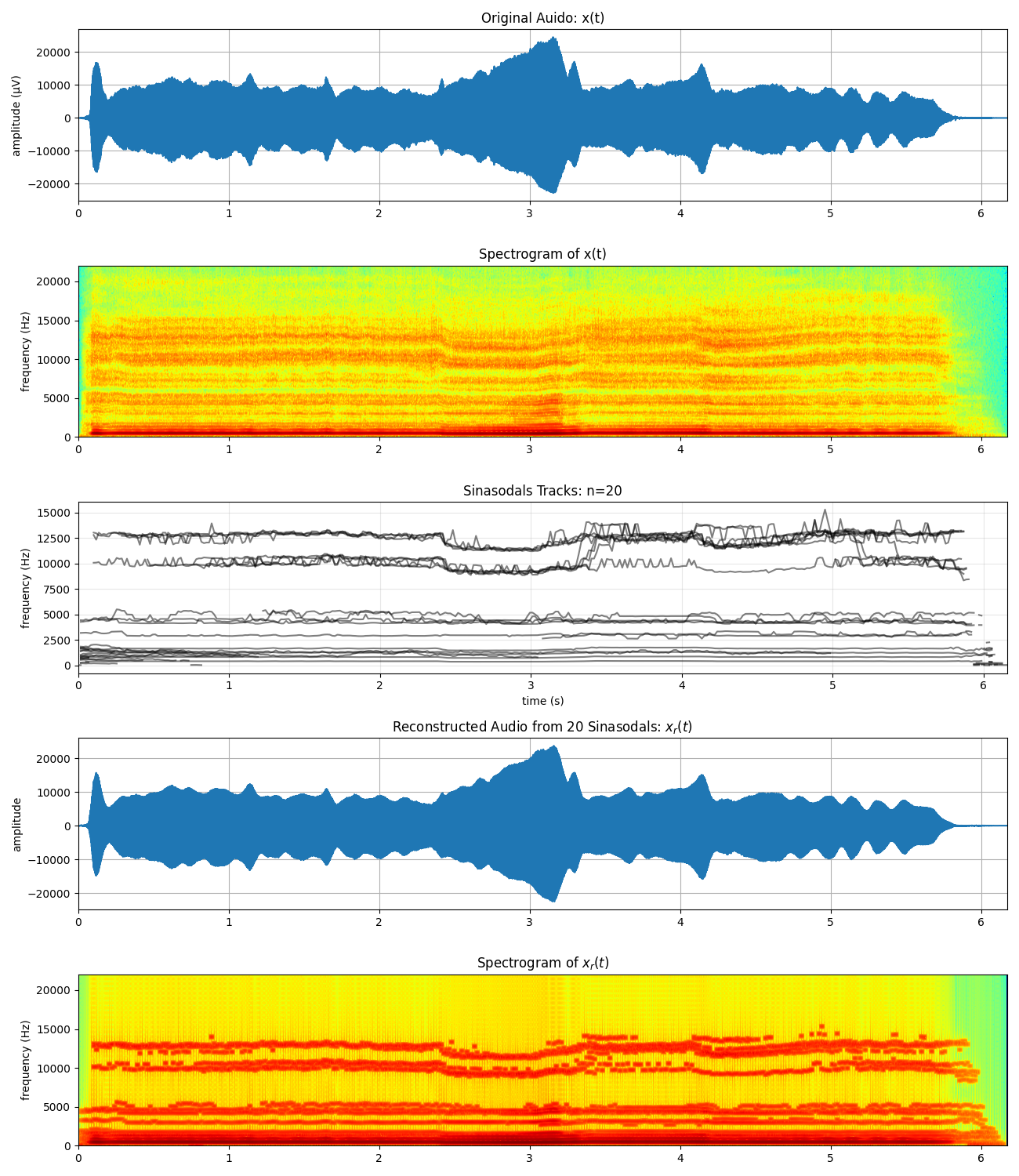
4 Sinasodual Model: Audio¶

# Reading audio file from url

import requests
from scipy.io import wavfile

#uncomment in jupyter-notebook
#import IPython

path1 = 'https://github.com/Nikeshbajaj/web-data/blob/main/sounds/violin-B3.wav?raw=true'
path2 = 'https://github.com/Nikeshbajaj/web-data/blob/main/sounds/singing-female.wav?raw=true'
print(path2)



req = requests.get(path2)
with open('myfile.wav', 'wb') as f:
        f.write(req.content)

fs, x = wavfile.read('myfile.wav')
t = np.arange(len(x))/fs
x=x.astype(float)
print(x.shape, fs)

#  Analysis: Decompising into N-sinasodal tracks


N=20

fXst, mXst, pXst = sp.sineModel_analysis(x,fs,winlen=3001,overlap=750,
                            window='blackmanharris', nfft=None, thr=-10,
                            maxn_sines=N,minDur=0.01, freq_devOffset=10,freq_devSlope=0.1)

print(fXst.shape, mXst.shape, pXst.shape)


# Synthesis of audio from N-sinasodal tracks


Xr = sp.sineModel_synthesis(fXst, mXst, pXst,fs,overlap=750,crop_end=False)
print(Xr.shape)

#  plots


plt.figure(figsize=(13,15))
plt.subplot(511)
plt.plot(t,x)
plt.xlim([t[0],t[-1]])
plt.grid()
plt.title('Original Auido: x(t)')
#plt.xlabel('time (s)')
plt.ylabel('amplitude (μV)')

mXt,pXt = sp.stft_analysis(x, winlen=441, overlap=220,window='blackmanharris',nfft=None)

plt.subplot(512)
plt.imshow(mXt.T,aspect='auto',origin='lower',cmap='jet',extent=[t[0],t[-1],0,fs/2])
plt.title('Spectrogram of x(t)')
#plt.xlabel('time (s)')
plt.ylabel('frequency (Hz)')


fXt1 = (fXst.copy())*(mXst>0)
fXt1[fXt1==0]=np.nan


plt.subplot(513)
tx = t[-1]*np.arange(fXt1.shape[0])/fXt1.shape[0]

plt.plot(tx,fXt1,'-k',alpha=0.5)
#plt.ylim([0,fs/2])
plt.xlim([0,tx[-1]])

plt.title(f'Sinasodals Tracks: n={N}')
plt.xlabel('time (s)')
plt.ylabel('frequency (Hz)')
plt.grid(alpha=0.3)



plt.subplot(514)
plt.plot(t,Xr[:len(t)])
plt.xlim([t[0],t[-1]])
plt.grid()
plt.title(f'Reconstructed Audio from {N} Sinasodals: $x_r(t)$')
#plt.xlabel('time (s)')
plt.ylabel('amplitude')


mXrt,pXrt = sp.stft_analysis(Xr, winlen=441, overlap=220,window='blackmanharris',nfft=None)

plt.subplot(515)
plt.imshow(mXrt.T,aspect='auto',origin='lower',cmap='jet',extent=[t[0],t[-1],0,fs/2])
plt.title(r'Spectrogram of $x_r(t)$')
#plt.xlabel('time (s)')
plt.ylabel('frequency (Hz)')
plt.tight_layout()
plt.show()

#uncomment in jupyter-notebook
#print('Original Audio: $x(t)$')
#display(IPython.display.Audio(x,rate=fs))

#print(f'Reconstructed Audio: $x_r(t)$')
#display(IPython.display.Audio(Xr,rate=fs))



wavfile.write('singing_female_recons.wav', rate=fs, data=Xr.astype('int16'))
wavfile.write('singing_female_residual.wav', rate=fs, data=(x-Xr[:len(x)]).astype('int16'))

Original Auido: x(t), Spectrogram of x(t), Sinasodals Tracks: n=20, Reconstructed Audio from 20 Sinasodals: $x_r(t)$, Spectrogram of $x_r(t)$

https://github.com/Nikeshbajaj/web-data/blob/main/sounds/singing-female.wav?raw=true
(272243,) 44100
(363, 20) (363, 20) (363, 20)
(273000,)

### saved audio files

embed_audio(‘singing_female_recons’, attribute = c(“controls”, “loop”))

# embed_audio('singing_female_recons', attribute = c("controls", "loop"))


# embed_audio('https://raw.githubusercontent.com/Nikeshbajaj/spkit/master/spkit/data/singing-female.wav', attribute = c("controls", "loop"))

# ![]('https://raw.githubusercontent.com/Nikeshbajaj/spkit/master/spkit/data/singing-female.wav')

# ![]('https://raw.githubusercontent.com/Nikeshbajaj/spkit/master/spkit/data/singing-female.wav')

# Original Audio
#
# <audio controls="controls">
#       <source src="https://raw.githubusercontent.com/Nikeshbajaj/spkit/master/spkit/data/singing-female.wav" type="audio/wav">
# </audio>
#
# https://raw.githubusercontent.com/Nikeshbajaj/spkit/master/spkit/data/singing-female.wav
#
#
# Reconstructed Audio
#
# <audio controls="controls">
#       <source src="https://raw.githubusercontent.com/Nikeshbajaj/spkit/master/spkit/data/singing_female_recons.wav" type="audio/wav">
# </audio>
#
# https://raw.githubusercontent.com/Nikeshbajaj/spkit/master/spkit/data/singing_female_recons.wav
#
#
# Residual Audio
# <audio controls="controls">
#       <source src="https://raw.githubusercontent.com/Nikeshbajaj/spkit/master/spkit/data/singing_female_residual.wav" type="audio/wav">
# </audio>
#
# https://raw.githubusercontent.com/Nikeshbajaj/spkit/master/spkit/data/singing_female_residual.wav