Note

Go to the end to download the full example code or to run this example in your browser via JupyterLite or Binder

Logistic Regression - Visualisation¶

An example of a Logistic Regression with visualasation

# ## libraries

import numpy as np
import matplotlib.pyplot as plt
import spkit
print('spkit version :', spkit.__version__)

from spkit.ml import LogisticRegression

spkit version : 0.0.9.7

Binary class

N = 300
np.random.seed(1)
X = np.random.randn(N,2)
y = np.random.randint(0,2,N)
y.sort()

# just creating classes a little far
X[y==0,:]+=2
print(X.shape, y.shape)


model = LogisticRegression(alpha=0.1)
model.fit(X,y,max_itr=1000)
yp  = model.predict(X)
ypr = model.predict_proba(X)
print('Accuracy : ',np.mean(yp==y))
print('Loss     : ',model.Loss(y,ypr))

plt.figure(figsize=(12,7))
ax1 = plt.subplot(221)
model.plot_Lcurve(ax=ax1)
ax2 = plt.subplot(222)
model.plot_boundries(X,y,ax=ax2)

ax3 = plt.subplot(223)
model.plot_weights(ax=ax3)
ax4 = plt.subplot(224)
model.plot_weights2(ax=ax4,grid=False)
plt.tight_layout()
plt.show()

# plt.plot(X[y==0,0],X[y==0,1],'.b')
# plt.plot(X[y==1,0],X[y==1,1],'.r')
# plt.tight_layout()
# plt.show()

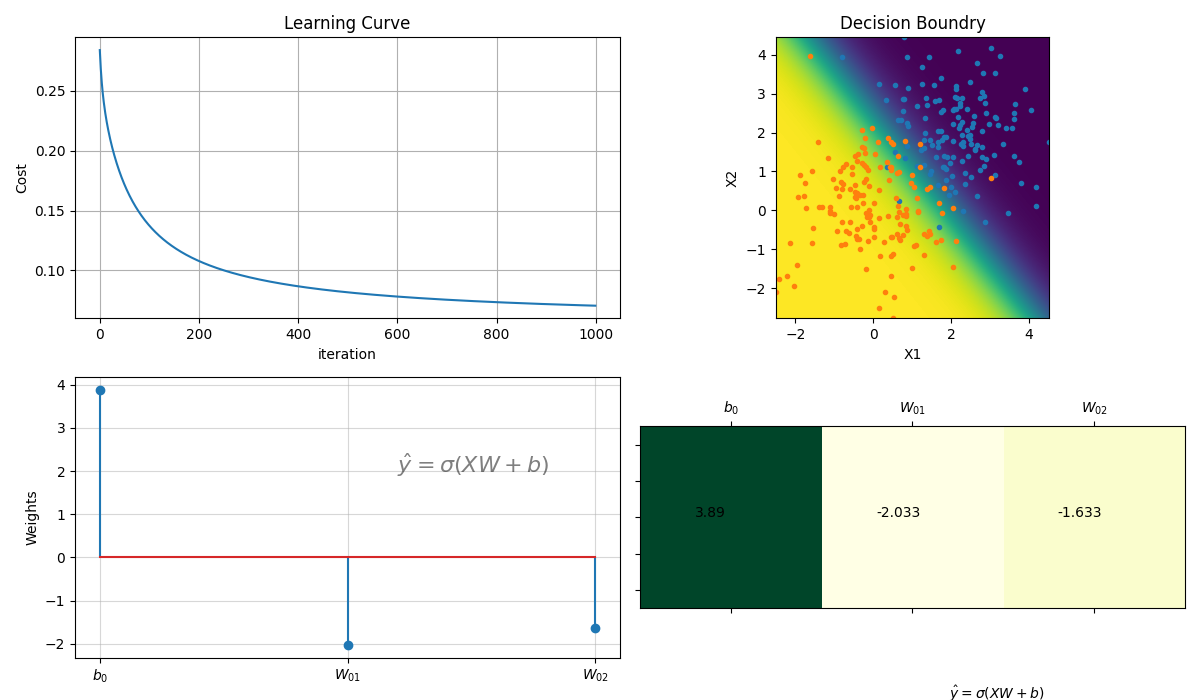
(300, 2) (300,)
Accuracy :  0.96
Loss     :  0.07046678918014998

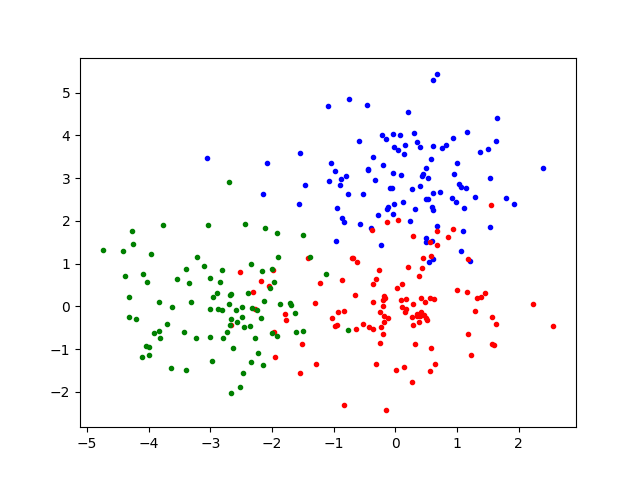
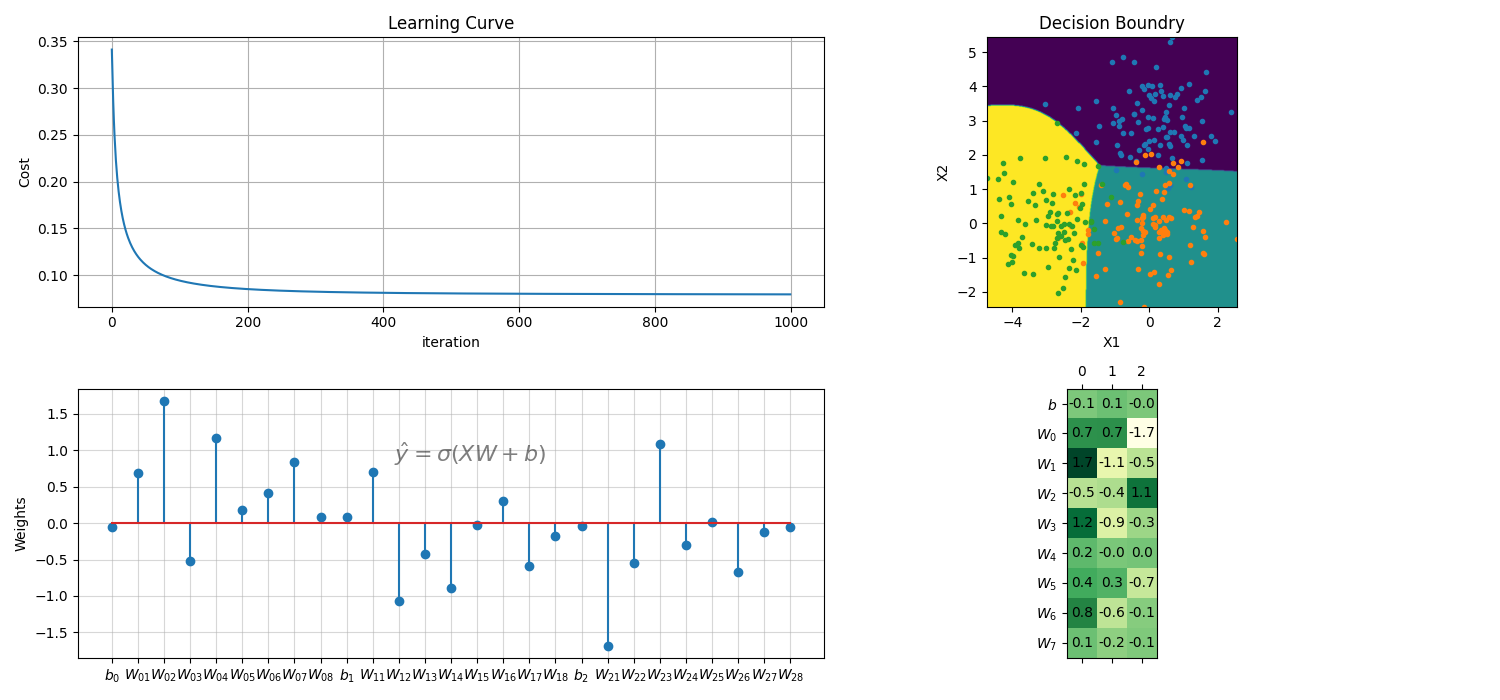
Multiclass with polynomial feature

N =300
X = np.random.randn(N,2)
y = np.random.randint(0,3,N)
y.sort()

X[y==0,1]+=3
X[y==2,0]-=3
print(X.shape, y.shape)

plt.plot(X[y==0,0],X[y==0,1],'.b')
plt.plot(X[y==1,0],X[y==1,1],'.r')
plt.plot(X[y==2,0],X[y==2,1],'.g')
plt.show()


model = LogisticRegression(alpha=0.1,polyfit=True,degree=3,lambd=0,FeatureNormalize=True)
model.fit(X,y,max_itr=1000)
yp  = model.predict(X)
ypr = model.predict_proba(X)
print(model)
print('')
print('Accuracy : ',np.mean(yp==y))
print('Loss     : ',model.Loss(model.oneHot(y),ypr))


plt.figure(figsize=(15,7))
ax1 = plt.subplot(221)
model.plot_Lcurve(ax=ax1)
ax2 = plt.subplot(222)
model.plot_boundries(X,y,ax=ax2)

ax3 = plt.subplot(223)
model.plot_weights(ax=ax3)
ax4 = plt.subplot(224)
model.plot_weights2(ax=ax4,grid=True)
plt.tight_layout()
plt.show()

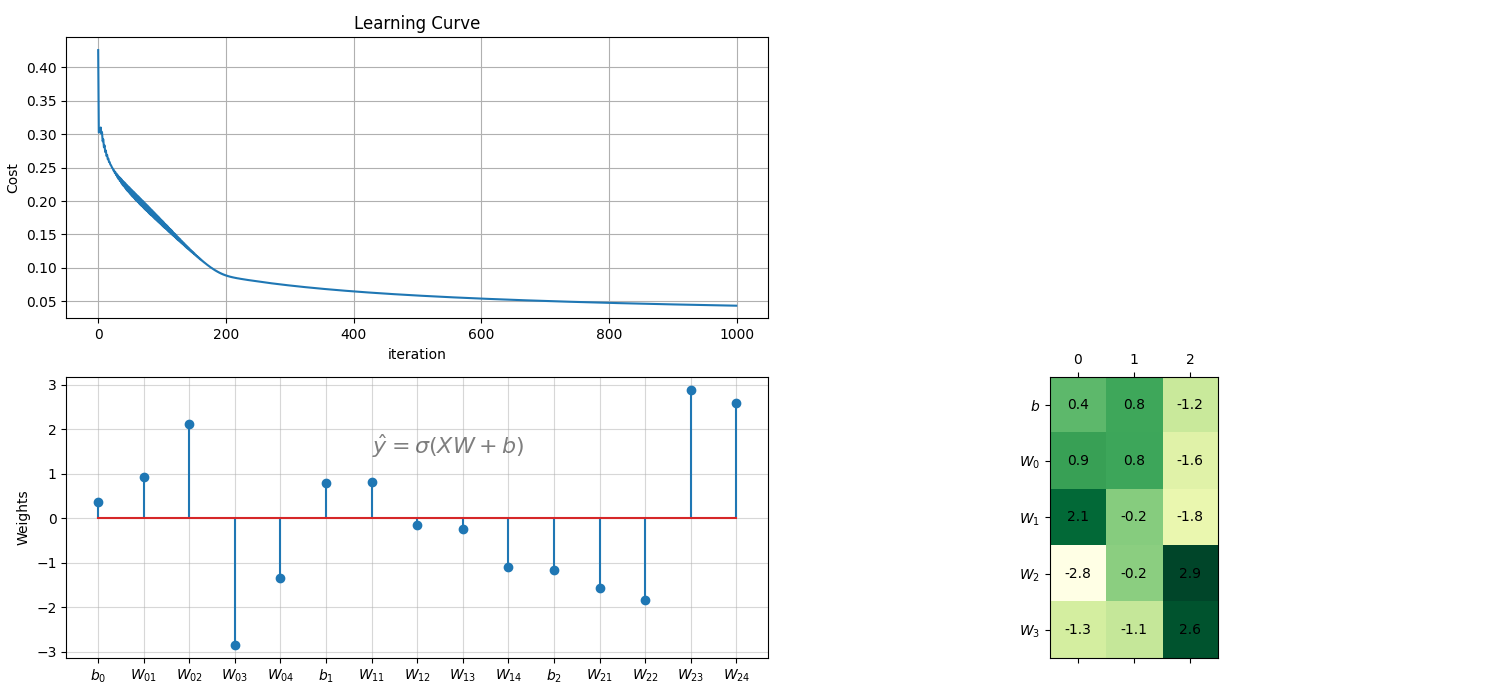
(300, 2) (300,)
LogisticRegression(alpha=0.1,lambd=0,polyfit=True,degree=3,FeatureNormalize=True,
         penalty=l2,tol=0.01,rho=0.9,C=1.0,fit_intercept=True)

Accuracy :  0.89
Loss     :  0.07928431824494166

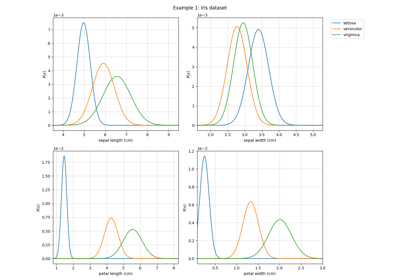
## Iris Dataset

from sklearn import datasets
from sklearn.model_selection import train_test_split


data = datasets.load_iris()
X = data.data
y = data.target

Xt,Xs, yt, ys = train_test_split(X,y,test_size=0.3)

print('Shapes ',X.shape,y.shape, Xt.shape, yt.shape, Xs.shape, ys.shape)


# # With polynomial features

model = LogisticRegression(alpha=0.1,polyfit=False,degree=3,lambd=0,FeatureNormalize=False)
model.fit(Xt,yt,max_itr=1000)

ytp  = model.predict(Xt)
ytpr = model.predict_proba(Xt)

ysp  = model.predict(Xs)
yspr = model.predict_proba(Xs)

print(model)

print('')
print('Training Accuracy : ',np.mean(ytp==yt))
print('Testing  Accuracy : ',np.mean(ysp==ys))
print('Training Loss     : ',model.Loss(model.oneHot(yt),ytpr))
print('Testing  Loss     : ',model.Loss(model.oneHot(ys),yspr))



plt.figure(figsize=(15,7))
ax1 = plt.subplot(221)
model.plot_Lcurve(ax=ax1)
ax3 = plt.subplot(223)
model.plot_weights(ax=ax3)
ax4 = plt.subplot(224)
model.plot_weights2(ax=ax4,grid=True)
plt.tight_layout()
plt.show()

Shapes  (150, 4) (150,) (105, 4) (105,) (45, 4) (45,)
LogisticRegression(alpha=0.1,lambd=0,polyfit=False,degree=3,FeatureNormalize=False,
         penalty=l2,tol=0.01,rho=0.9,C=1.0,fit_intercept=True)

Training Accuracy :  0.9714285714285714
Testing  Accuracy :  0.9777777777777777
Training Loss     :  0.04372580813833042
Testing  Loss     :  0.03776786129832711

Total running time of the script: (0 minutes 1.124 seconds)