Note
Go to the end to download the full example code or to run this example in your browser via JupyterLite or Binder
Testing two groups¶
#sp.stats.test_2groups
Example 1: Paired¶
import numpy as np
import matplotlib.pyplot as plt
import spkit as sp
np.random.seed(1)
x1 = np.random.randn(100)
x2 = np.random.randn(100)+0.2
tPass,(df1,df2) = sp.stats.test_2groups(x1,x2,paired=True,alpha=0.05,title=None,tval=True,
printthr=1,return_all=True,print_round=4,notes=True,pre_tests=True,effect_size=True,
plots=True)
print('Test Result Table')
print(df1)
print('Test Effect-size')
print(df2)
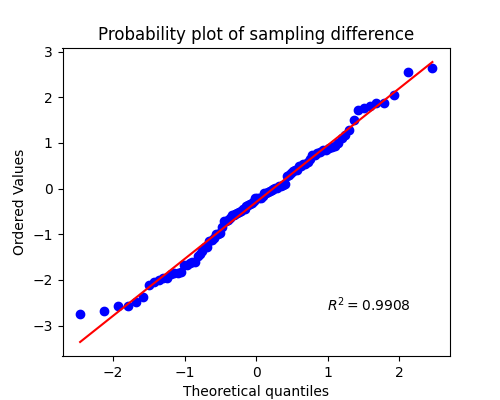
Test for Normality
--------------------------------------------------
Shapiro-test on diff
p-value: 0.408 - with stats 0.9865 | Pass
If test is not significant (p<alpha) that indicates the sampling distribution is normally distributed.
Effect Size
--------------------------------------------------
Mean diff (x1-x2): -0.2922
CohensD (x1-x2): -0.3199
==================================================
Final Test
==================================================
Test p-value (stats) |(n=100)
--------------------------------------------------
T-test paired 0.0196 (stats= -2.3719)
Wilcoxon signed-rank 0.028 (stats= 1886.0)
==================================================
Test Result Table
p-value stats
shapiro 0.407988 0.986549
t-test 0.019631 -2.371901
wilcox 0.028014 1886.000000
Test Effect-size
mean_diff CohensD
effect_size -0.292212 -0.319897
Example 2: Unpaired¶
import numpy as np
import matplotlib.pyplot as plt
import spkit as sp
np.random.seed(1)
x1 = np.random.randn(10)
x2 = np.random.randn(11)+0
tPass,(df1,df2) = sp.stats.test_2groups(x1,x2,paired=False,alpha=0.05,title=None,tval=True,
printthr=1,return_all=True,
print_round=4,notes=True,pre_tests=True,effect_size=True,plots=True)
print('Test Result Table')
print(df1)
print('Test Effect-size')
print(df2)
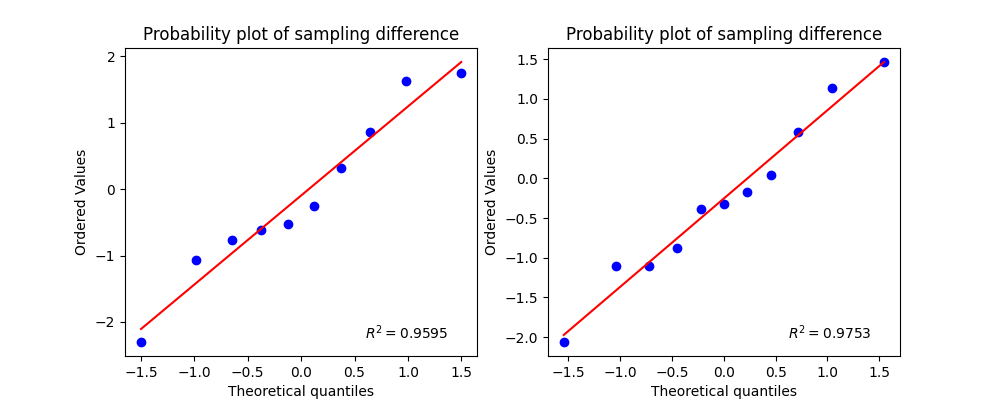
Test for Normality
--------------------------------------------------
Shapiro-test
x1: p-value 0.7441: with stats 0.9564 | Pass
x2: p-value 0.9299: with stats 0.9747 | Pass
If test is not significant (p<alpha) that indicates the sampling distribution is normally distributed.
Test for Homogeneity of Variance
--------------------------------------------------
Levene test
p-value 0.5793: with stats 0.3182 | Pass
The small p-value suggests that the populations do not have equal variances
Effect Size
--------------------------------------------------
Mean diff (x1-x2): 0.1571
CohensD (x1-x2): 0.1371
==================================================
Final Test
==================================================
Test p-value (stats) |(n1=10, n2=11)
--------------------------------------------------
T-test indept. 0.7572 (stats= 0.3137)
Wilcoxon rank-sum 0.7248 (stats= 0.3521)
==================================================
Test Result Table
p-value stats
shapiro_x1 0.744053 0.956390
shapiro_x2 0.929865 0.974728
levene 0.579284 0.318210
t-test 0.757153 0.313718
ranksum 0.724771 0.352089
Test Effect-size
mean_diff CohensD
effect_size 0.157087 0.137073
Total running time of the script: (0 minutes 0.127 seconds)
Related examples
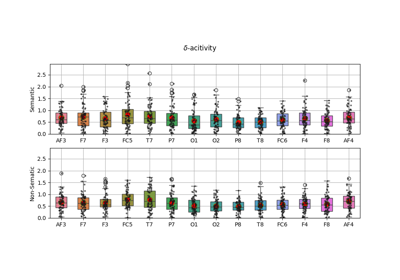
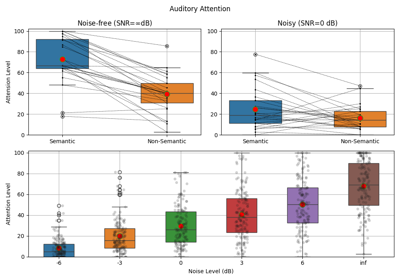
EEG Computing Rhythmic Features - PhyAAt - Semanticity
EEG Computing Rhythmic Features - PhyAAt - Semanticity