Note

Go to the end to download the full example code or to run this example in your browser via JupyterLite or Binder

Dispersion Entropy with top patterns¶

Dispersion Entropy is computed by first discretising the signal and then extracting all the dispersing patterns of given embedding dimension. The ditrubution of patterns determines the dispersion entropy of signal. If signal have a few patterns with high repetitions compare to others signal is less random which entails the low entropy. On the other hand, a random signal with no patterns repetitions more than others leads to high entropy.

import numpy as np
import matplotlib.pyplot as plt
import spkit as sp
print('spkit-version',sp.__version__)

spkit-version 0.0.9.7

load sample EEG Signal

X,fs,ch_names = sp.data.eeg_sample_14ch()

Xi = sp.filter_X(X[:,0],band=[1,20],btype='bandpass',verbose=0)
print('EEG Sample : Shape',Xi.shape)
t = np.arange(Xi.shape[0])/fs

EEG Sample : Shape (2048,)

Dispersion Entropy

print('Dispersion Entropy with embeding dimention=4')
print('-'*10)

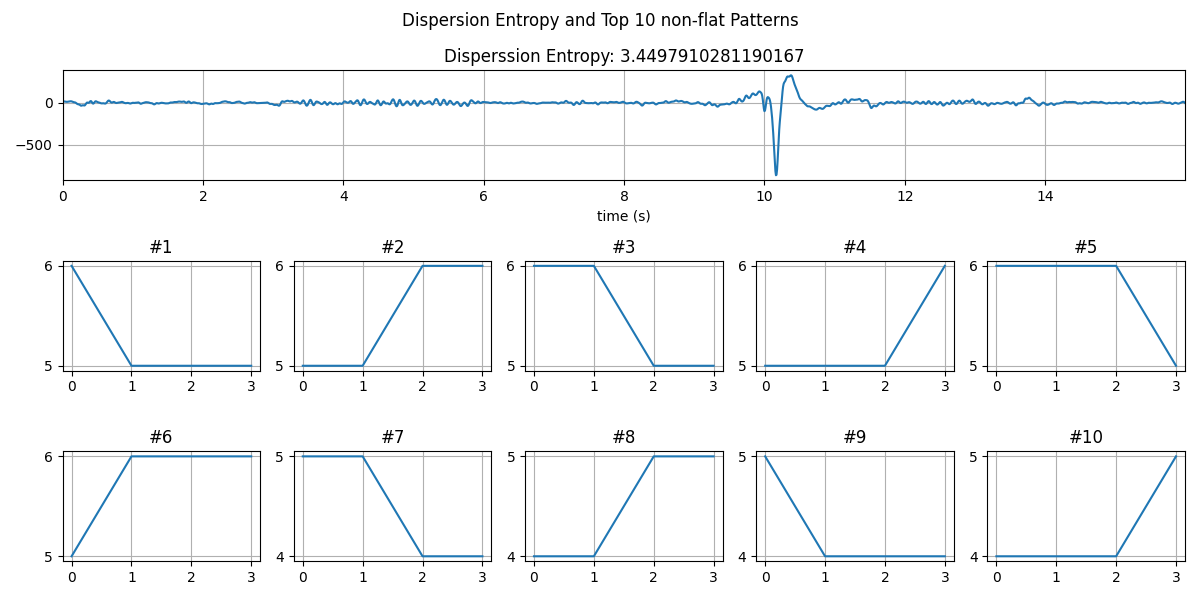
de,prob,patterns_dict,_,_= sp.dispersion_entropy(Xi,classes=10, scale=1, emb_dim=4, delay=1,return_all=True)
print('Disperssion Entropy: ',de)



PP = np.array([list(k)+[patterns_dict[k]] for k in patterns_dict])
idx = np.argsort(PP[:,-1])[::-1]
print('Top 10 Patterns')
print(PP[idx[:10],:-1])

Ptop = np.array(list(PP[idx,:-1]))
idx2 = np.where(np.sum(np.abs(Ptop-Ptop.mean(1)[:,None]),1)>0)[0]

fig = plt.figure(figsize=(12,6))
plt.subplot(3,1,1)
plt.plot(t,Xi)
plt.xlim([0,t[-1]])
plt.xlabel('time (s)')
plt.grid()
plt.title(f'Disperssion Entropy: {de}')
#plt.ylabel('Signal')
for i in range(10):
    plt.subplot(3,5,i+6)
    plt.plot(Ptop[idx2[i]].astype(int))
    plt.grid()
    plt.yticks(np.unique(Ptop[idx2[i]]))
    plt.title(f'#{i+1}')

fig.suptitle('Dispersion Entropy and Top 10 non-flat Patterns')
plt.tight_layout()
plt.show()


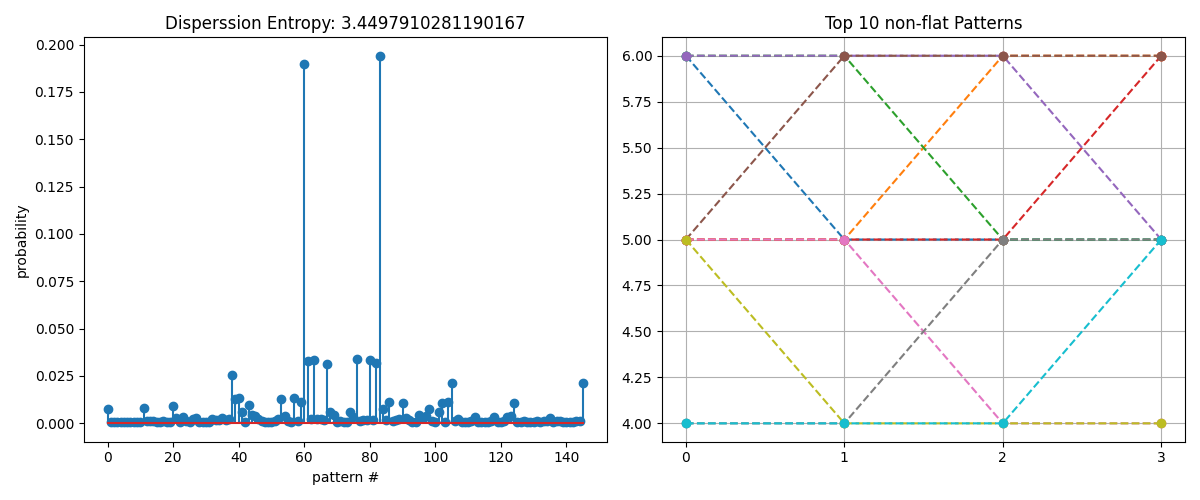
fig = plt.figure(figsize=(12,5))
plt.subplot(121)
plt.stem(np.arange(len(prob)),prob)
plt.xlabel('pattern #')
plt.ylabel('probability')
plt.title(f'Disperssion Entropy: {de}')
plt.subplot(122)
plt.plot(Ptop[idx2[:10]].T,'--o')
plt.xticks([0,1,2,3])
plt.grid()
plt.title('Top 10 non-flat Patterns')
plt.tight_layout()
plt.show()

Dispersion Entropy with embeding dimention=4
----------
Disperssion Entropy:  3.4497910281190167
Top 10 Patterns
[[6 6 6 6]
 [5 5 5 5]
 [6 5 5 5]
 [5 5 6 6]
 [6 6 5 5]
 [5 5 5 6]
 [6 6 6 5]
 [5 6 6 6]
 [4 4 4 4]
 [7 7 7 7]]

Total running time of the script: (0 minutes 0.585 seconds)