spkit.eeg.ATAR

spkit.eeg.ATAR(X, wv='db3', winsize=128, thr_method='ipr', OptMode='soft', IPR=[25, 75], beta=0.1, k1=10, k2=100, est_wmax=100, theta_a=inf, bf=2, gf=0.8, wpd_mode='symmetric', wpd_maxlevel=None, recons_method='atar-style', window=['hamming', True], hopesize=None, packetwise=False, WPD=True, lvl=[], use_joblib=False, verbose=False, bound_warn=True, **kwargs)

ATAR - Automatic and Tunable Artifact Removal Algorithm

ATAR: - Automatic and Tunable Artifact Removal Algorithm

Apply ATAR on short windows of signal (single channel):

Signal is decomposed in smaller overlapping windows and reconstructed after correcting using overlap-add method.

For more details, check [1]

Operating Modes

1. Soft Thresholding

\[ \begin{align}\begin{aligned}\lambda_s (w) &= w & \quad \text{if } |w|<\theta_{\gamma}\\ &= \theta_{\alpha} \frac{1 - e^{\alpha w}}{1 + e^{\alpha w}} & \quad \text{otherwise}\end{aligned}\end{align} \]

2. Elimination

\[ \begin{align}\begin{aligned}\lambda_e (w) &= w & \quad \text{if } |w| \le \theta_{\alpha}\\ &= 0 & \quad \text{otherwise}\end{aligned}\end{align} \]

3. Linear Attenuation

\[ \begin{align}\begin{aligned}\lambda_a (w) &= w & \quad \text{if } |w| \le \theta_{\alpha}\\ &= sgn(w) \theta_{\alpha} \Big( 1 - \frac{|w| - \theta_{\alpha}}{\theta_{\beta}-\theta_{\alpha}} \Big) & \quad \text{if } \theta_{\alpha} < |w| \le \theta_{\beta}\\ &= 0 & \quad \text{otherwise}\end{aligned}\end{align} \]

Computing Threshold

  • \(f_{\beta}(r) = k_2 \cdot exp \Big(-\beta \frac{w_{max}}{k_2} \times \frac{r}{2} \Big)\)

  • \(\theta_{\alpha} = f_{\beta}(r) \quad \text{if } f_{\beta}(r) \ge k_1\) otherwise \(\theta_{\alpha} = k_1\)

  • \(\theta_{\gamma} = g_f \times \theta_{\alpha}\) , where a default value for ‘g_f = 0.8’ For Soft-threshold

  • \(\theta_{\beta} = b_f \times \theta_{\alpha}\) , where a default value for ‘b_f = 2’ For Linear Attenuation

Parameters:
x1d-array

  • input single-channel signal of shape (n,)

wv = str, ‘db3’(default) wavelet
  • one of wavelet family {‘db3’…..’db38’, ‘sym2…..sym20’,

    ‘coif1…..coif17’, ‘bior1.1….bior6.8’,

    ‘rbio1.1…rbio6.8’, ‘dmey’}

winsize: int, deafult=128

  • window size to apply ATAR

hopesize: int, None, default=None,

  • overlap shift for next window

  • if None, hopesize=winsize//2

  • only used when recons_method={‘atar-style’,’atar’,’custom’}

Operating modes
OptMode: str, {‘soft’,’elim’,’linAtten’}, default ‘soft’

  • Operating Modes:

  • soft: soft-thresholding (need theta_a, and theta_g)

  • elim: Elimination mode (need theta_a)

  • linAtten: Linear Attenuation mode (need theta_a and theta_b)

    • given bf and gf (default bf = 2, gf=0.8)

    • where:-

      • theta_b = bf*theta_a – used for Linear Attenuation

      • theta_g = gf*theta_a – used for Soft thresholding

*Threshold Computation method*
thr_method: str, {‘ipr’, None}

  • Computing method for threshold

  • if ‘ipr’ ‘theta_a’ is computed as per ATAR’s approach

  • if None, passed value of ‘theta_a’ is used along with (bf, gf)

IPR: list of two default=[25,75]

  • To compute Interpercentile range r

  • e.g. [10,90], [30,70]

  • Higher the range is, threshold is more affected by outliers

  • Interpercentile range r is mapped to threshold, using beta, k1 and k2

beta: float (0,1] default=0.1

  • beta as tuning parameter for threshold

  • higher the value, more aggressive is the algorithm to remove artifacts

(k1,k2) :scalars, defualt (10,100)

  • lower and upper bounds on the threshold value

  • should be of same order as signal magnitude.

  • if signal is in volts, values will be of order 1e-6, then k1 and k2 should be around those order

  • defult values k1=10, k2=100 are chosen for signal with unit of microVolt (uV), of order of 100s

Warning

k1,k2 bounds if k2 is very high (e.g. 100) and signal amplitude is in 1e-3, 1e-6, ATAR will have no effect on the signal, as theshold to identify and remove artifacts will be so high.

est_wmax: int, default=100

  • est_wmax is the value in the expression (15 in paper) or above Computing Threshold equations w_max

*Wavelet Decomposition*
wpd_mode: str, default ‘symmetric’
  • one of the {‘zero’, ‘constant’, ‘symmetric’, ‘periodic’,

    ‘smooth’, ‘periodization’}

wpd_maxlevel: int, defualt=None

  • maximum number of levels for decomposition,

  • if None, max possible number of level are used.

use_joblib: bool, default=False

  • If True, joblib is used for parallel processing of the channels

verbose: int

  • vebosity level

Experimental Settings

Note

NOT RECOMMONEDED TO CHANGE Following parameters are experimental, they are not recommonded to change, and leave as default

WPD: bool, default=True

  • if False Wavelet Transform is used for decompisiton of signal, else Wavelet Packet Decomposition is used

packetwise: bool, deafult=False

  • if True, threshold is computed and applied to each packet independently.

lvl: list defualt=[]

  • if provided, ATAR is applied to provided level numbers only.

recons_method: str deafult=’atar-style’

  • reconstruction method after applying atar to each window.

  • one of {‘atar-style’, ‘atar’, ‘custom’, ‘HamWin’,’Hamming’}

Note

NOT RECOMMONEDED TO CHANGE KEEP IT TO DEFAULT

window: list of two default=[‘hamming’,True]

  • window function, and if windowing is applied before or after atar

Returns:
XR: corrected signal of same shape as input X

See also

ATAR_1Ch

ATAR for single channel

ATAR_mCh

ATAR for multiple channel

ICA_filtering

ICA based Artifact Removal Algorithm

References

[1]

Bajaj, Nikesh, et al. “Automatic and tunable algorithm for EEG artifact removal using wavelet decomposition with applications in predictive modeling during auditory tasks.” Biomedical Signal Processing and Control 55 (2020): 101624. https://doi.org/10.1016/j.bspc.2019.101624

Examples

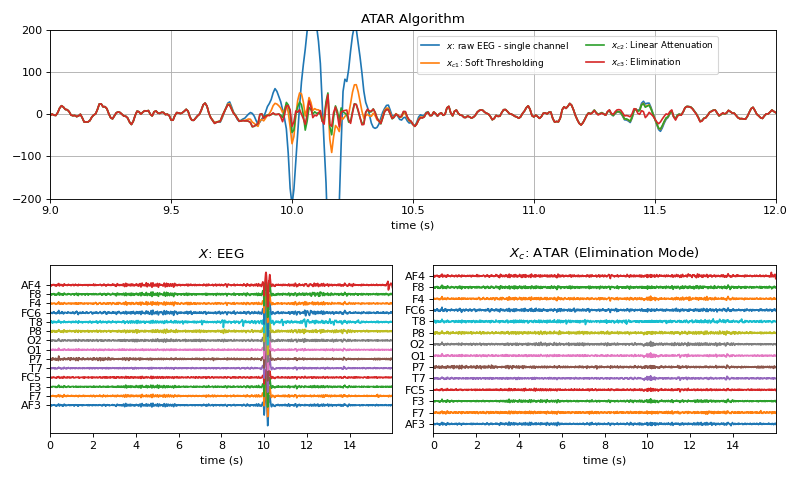
#sp.eeg.ATAR
import numpy as np
import matplotlib.pyplot as plt
import spkit as sp
X,fs, ch_names = sp.data.eeg_sample_14ch()
X = sp.filterDC_sGolay(X, window_length=fs//3+1)
t = np.arange(X.shape[0])/fs
# Single Channel
x = X[:,0] 
xc1 = sp.eeg.ATAR(x,wv='db3', winsize=128, thr_method='ipr',beta=0.1, k1=10, k2=100,OptMode='soft',verbose=1)
xc2 = sp.eeg.ATAR(x,wv='db3', winsize=128, thr_method='ipr',beta=0.1, k1=10, k2=100,OptMode='linAtten',verbose=1)
xc3 = sp.eeg.ATAR(x,wv='db3', winsize=128, thr_method='ipr',beta=0.1, k1=10, k2=100,OptMode='elim',verbose=1)
# Multi-Channel
Xc = sp.eeg.ATAR(X,wv='db3', winsize=128, thr_method='ipr',beta=0.2, k1=10, k2=100,OptMode='elim')
sep=200
plt.figure(figsize=(10,6))
plt.subplot(211)
plt.plot(t,x, label='$x$: raw EEG - single channel')
plt.plot(t,xc1,label=r'$x_{c1}$: Soft Thresholding')
plt.plot(t,xc2,label=r'$x_{c2}$: Linear Attenuation')
plt.plot(t,xc3,label=r'$x_{c3}$: Elimination')
plt.xlim([9,12])
plt.ylim([-200,200])
plt.legend(bbox_to_anchor=(0.5,0.99),ncol=2,fontsize=8)
plt.grid()
plt.title(r'ATAR Algorithm')
plt.xlabel('time (s)')
plt.subplot(223)
plt.plot(t,X+np.arange(X.shape[1])*sep)
plt.xlim([t[0],t[-1]])
plt.yticks(np.arange(X.shape[1])*sep,ch_names)
plt.title(r'$X$: EEG')
plt.xlabel('time (s)')
plt.subplot(224)
plt.plot(t,Xc+np.arange(14)*sep)
plt.xlim([t[0],t[-1]])
plt.title(r'$X_c$: ATAR (Elimination Mode)')
plt.yticks(np.arange(X.shape[1])*sep,ch_names)
plt.xlabel('time (s)')
plt.tight_layout()
plt.show()
../../_images/spkit-eeg-ATAR-1.png

Examples using spkit.eeg.ATAR

ATAR Algorithm with MNE RAW Object

ATAR Algorithm with MNE RAW Object