spkit.conv1d_nan

spkit.conv1d_nan(x, kernel, denormalise_ker=True, boundary='constant', fillvalue=nan)

1D Convolution with NaN values

1D Convolution with NaN values

In conventional Convolution funtions, if any of the value in input x or in kernel is NaN (np.nan), then NaN values are propogated and corrupt other values too.

To avoid this, this funtion does the convolution in same fashion as conventional except, it allows NaN values to exists in input, without propogating them.

while computation, it simply ignores the NaN value, as it doen not exist, and adjust the computation accordingly.

If No NaN value exist, result is same as conventional convolution

Parameters:

x1d-array,

• input signal single channel (n,) with NaN values.

kernel: a 1D kernel

• to use for convolution

• IMPORTANT NOTE: kernel passed should NOT be normalised. If normalised kernel is used, the results will be very different than conventional convolution. For example:

  kernel_unnorm = np.ones(9) kernel_norm = np.ones(9)/9

  kernel_unnorm should be passed, not kernel_norm.

• To de-normalise a kernel, used denorm_kernel

• or set denormalise_ker=True

denormalise_ker: bool, default=True

• If True, first de-normalise kernel

boundarystr {‘fill’,’constant’ ,’wrap’, ‘symm’,’symmetric’,’reflect’,}, optional

A flag indicating how to handle boundaries:

fill or constant

pad input arrays with fillvalue. (default)

wrap

circular boundary conditions.

symm or ‘symmetric’

symmetrical boundary conditions.

reflect

reflecting boundary conditions.

fillvalue: scalar, optional

• Value to fill pad input arrays with. Default is np.nan,

Returns:

y: 1D-arrray

• of same size as input x with no NaN propogation

See also

conv2d_nan

2D Convolution with NaN

fill_nans_1d

fill NaN of 1d array

fill_nans_2d

fill NaN of 2d array

Notes

See examples below

Examples

>>> #sp.conv1d_nan
>>> import numpy as np
>>> import spkit as sp
>>> from scipy import signal
>>> N = 10
>>> np.random.seed(seed=200)
>>> X  = np.random.randint(0,5,N)
>>> r = 1*(np.abs(np.random.randn(N))<1.4).astype(float)
>>> r[r==0]=np.nan
>>> X_nan = X*r
>>> kernel_norm = np.ones(9)/9
>>> cx1 = signal.convolve(X_nan,kernel_norm, method='auto',mode='same')
>>> cx2 = sp.conv1d_nan(X_nan,kernel_norm, denormalise_ker=True)
>>> print('Convolution kernel: ')
>>> print(' - ',kernel_norm.round(3))
>>> print('input signal with Nans')
>>> print(' - ',X_nan)
>>> print('Convolution using scipy')
>>> print(' - ',cx1.round(3))
>>> print('Convolution using spkit')
>>> print(' - ',cx2.round(3))

>>> ####################################################
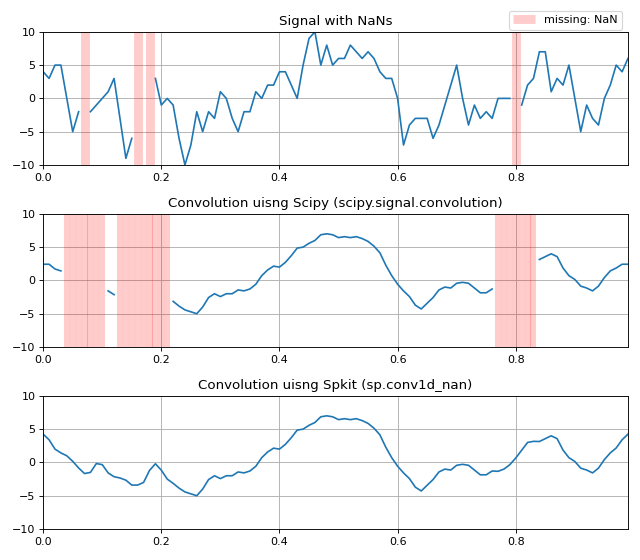
>>> #sp.conv1d_nan
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> import scipy
>>> import spkit as sp
>>> seed = 4
>>> x = (sp.create_signal_1d(n=100,seed=seed,sg_winlen=5)*10).round(0)
>>> t = np.arange(len(x))/100
>>> np.random.seed(seed)
>>> r = np.random.rand(*x.shape)
>>> x[r<0.05] = np.nan
>>> kernel = np.ones(7)/7
>>> np.random.seed(None)
>>> x_scipy = scipy.signal.convolve(x.copy(), kernel,mode='same')
>>> x_spkit = sp.conv1d_nan(x.copy(), kernel)
>>> plt.figure(figsize=(8,7))
>>> plt.subplot(311)
>>> plt.plot(t,x,color='C0')
>>> plt.vlines(t[np.isnan(x)],ymin=np.nanmin(x),ymax=np.nanmax(x),color='r',alpha=0.2,lw=8,label='missing: NaN')
>>> plt.xlim([t[0],t[-1]])
>>> plt.ylim([np.nanmin(x),np.nanmax(x)])
>>> plt.legend(bbox_to_anchor=(1,1.2))
>>> plt.grid()
>>> plt.title('Signal with NaNs')
>>> plt.subplot(312)
>>> plt.plot(t,x_scipy)
>>> plt.vlines(t[np.isnan(x_scipy)],ymin=np.nanmin(x),ymax=np.nanmax(x),color='r',alpha=0.2,lw=5.5)
>>> plt.xlim([t[0],t[-1]])
>>> plt.ylim([np.nanmin(x),np.nanmax(x)])
>>> plt.grid()
>>> plt.title('Convolution uisng Scipy (scipy.signal.convolution)')
>>> plt.subplot(313)
>>> plt.plot(t,x_spkit)
>>> plt.xlim([t[0],t[-1]])
>>> plt.ylim([np.nanmin(x),np.nanmax(x)])
>>> plt.grid()
>>> plt.title('Convolution uisng Spkit (sp.conv1d_nan)')
>>> plt.tight_layout()
>>> plt.show()

Examples using spkit.conv1d_nan

Release Highlights for spkit 0.0.9.7

Release Highlights for spkit 0.0.9.7