Note

Go to the end to download the full example code or to run this example in your browser via JupyterLite or Binder

Ramanujan Dictionary - with sparse penalty¶

import numpy as np
import matplotlib.pyplot as plt
import sys, scipy
from scipy import linalg as LA
import spkit as sp
print('spkit version :', sp.__version__)


# # Ramanujan Dictionary  - with sparse penalty

spkit version : 0.0.9.7

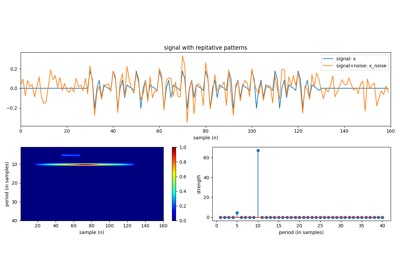
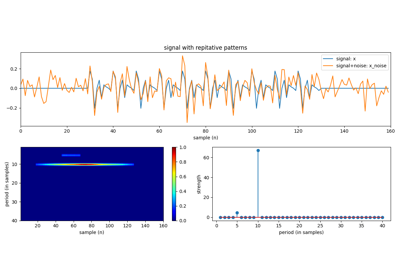
Signal with 3-periods and SNR=10¶

#np.random.seed(None)

periods    = [3,7,11]
signal_length = 200
SNR = 10

x = np.zeros(signal_length)

for period in periods:
    x_temp  = np.random.randn(period)
    x_temp  = np.tile(x_temp,int(np.ceil(signal_length/period)))
    x_temp  = x_temp[:signal_length]
    x_temp /= LA.norm(x_temp,2)
    x += x_temp

x_noise = sp.add_noise(x,snr_db=SNR)

Pmax = 80

# L1 regularisation with sparse penalty
period_est_l1_1l = sp.regularised_period_estimation(x_noise,Pmax=Pmax,method='Ramanujan',lambd=1, L=1, cvxsol=True)

# L1 regularisation with no penalty
period_est_l1_0l = sp.regularised_period_estimation(x_noise,Pmax=Pmax,method='Ramanujan',lambd=0, L=1, cvxsol=True)

# L2 regularisation with sparse penalty
period_est_l2_1l = sp.regularised_period_estimation(x_noise,Pmax=Pmax,method='Ramanujan',lambd=1, L=2, cvxsol=False)

# No regularisation no  penalty
y =  sp.ramanujan_filter(x_noise,Pmax = Pmax, Rcq=10, Rav=2, Th=0.2)
period_est_rbf  = np.sum(y,0)

print('Top 10 periods : ')
print(' - using L1 regularisation with sparse penalty    : ',np.argsort(period_est_l1_1l)[::-1][:10]+1)
print(' - using L1 regularisation with no penalty : ',np.argsort(period_est_l1_0l)[::-1][:10]+1)
print(' - using L2 regularisation with sparse penalty    : ',np.argsort(period_est_l2_1l)[::-1][:10]+1)
print(' - using no regularisation no  penalty     : ',np.argsort(period_est_rbf)[::-1][:10]+1)

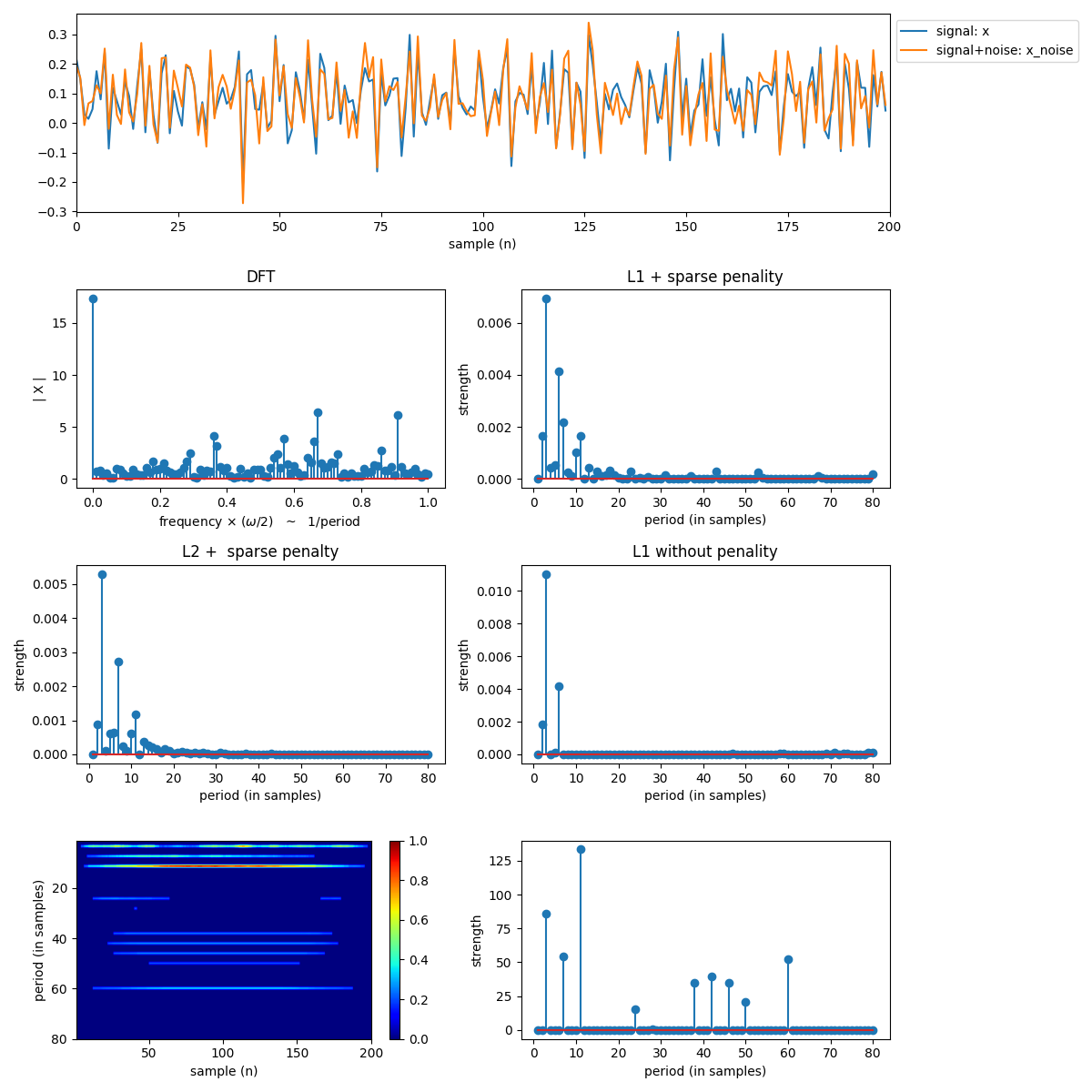
plt.figure(figsize=(12,12))
plt.subplot(411)
plt.plot(x,label='signal: x')
plt.plot(x_noise, label='signal+noise: x_noise')
#plt.text(5,1.01*np.max(x_noise) ,f'signal with repitative patterns')
plt.xlim([0,len(x)])
plt.xlabel('sample (n)')
plt.legend(bbox_to_anchor=(1,1))
plt.subplot(423)
XF = np.abs(np.fft.fft(x_noise))[:1+len(x_noise)//2]
fq = np.arange(len(XF))/(len(XF)-1)
plt.stem(fq,XF)
plt.title('DFT')
plt.ylabel('| X |')
plt.xlabel(r'frequency $\times$ ($\omega$/2)   ~   1/period ')

plt.subplot(424)
plt.stem(np.arange(len(period_est_l1_1l))+1,period_est_l1_1l)
plt.xlabel('period (in samples)')
plt.ylabel('strength')
plt.title('L1 + sparse penality')

plt.subplot(425)
plt.stem(np.arange(len(period_est_l2_1l))+1,period_est_l2_1l)
plt.xlabel('period (in samples)')
plt.ylabel('strength')
plt.title('L2 +  sparse penalty')
plt.subplot(426)
plt.stem(np.arange(len(period_est_l1_0l))+1,period_est_l1_0l)
plt.xlabel('period (in samples)')
plt.ylabel('strength')
plt.title('L1 without penality')


plt.subplot(427)
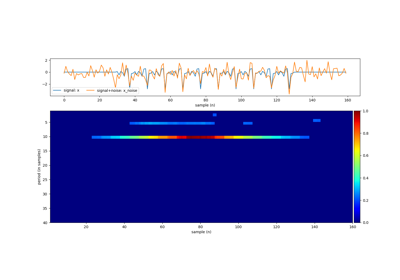
im = plt.imshow(y.T,aspect='auto',cmap='jet',extent=[1,len(x_noise),Pmax,1])
plt.colorbar(im)
plt.xlabel('sample (n)')
plt.ylabel('period (in samples)')

plt.subplot(428)
plt.stem(np.arange(1,y.shape[1]+1),period_est_rbf)
plt.xlabel('period (in samples)')
plt.ylabel('strength')
plt.tight_layout()
plt.show()

DFT, L1 + sparse penality, L2 + sparse penalty, L1 without penality

Top 10 periods :
 - using L1 regularisation with sparse penalty    :  [ 3  6  7 11  2 10  5 13  4 18]
 - using L1 regularisation with no penalty :  [ 3  6  2 79 80 71  5 73 59 69]
 - using L2 regularisation with sparse penalty    :  [ 3  7 11  2  6 10  5 13 14  8]
 - using no regularisation no  penalty     :  [11  3  7 60 42 38 46 50 24 28]

Total running time of the script: (0 minutes 3.771 seconds)