spkit.signal_diff

spkit.signal_diff(x, method='fdiff', sg_window=101, sg_polyorder=1, gauss_window=0, gauss_itr=1, gauss_sigscale=2.7, dt=1)

Derivative of a signal

Derivative of a signal

Computing Derivating of a signal is very useful in signal processing. In some of the physiological signals derivative of signal allows to compute events such as activation and repolarisation time.

This function implements some of the well known approaches to compute derivative

‘fdiff’:

  • Finite differentiation using first principle

intermediate values

\[dx(t) = [x(t+d) - x(t-d)]/2 \quad \text{when t+d and t-d in D (Domain)}\]

boundries

  • first point t=0, when t+d in D, but t-d not in D

\[ \begin{align}\begin{aligned}dx(t) &= x(t+d)-x(t)\\dx(0) &= x(d)-x(0)\end{aligned}\end{align} \]

  • last point t=l, when t-d in D, but t+d not in D

\[ \begin{align}\begin{aligned}dx(t) &= x(t)-x(t-d)\\dx(l) &= x(l)-x(l-d)\end{aligned}\end{align} \]
‘fgrad’:

  • Finite differentiation

  • Using finite gradient (np.gradient)

Note

fgrad is essentially the same as fdiff computed in numpy using np.gradient

for following methods:

  • parameters for Savitzky-Golay filter (sg_window , sg_polyorder)

  • parameters for gaussian kernal+ConvFB (gauss_window, gauss_itr ), applied only if gauss_window>0

‘sgdiff’:

  • Computing derivetive of signal using Savitzky-Golay filter,

  • then with gaussian kernal using Forward-Backward-Convolution (ConvFB).

‘sgdrift_diff’:

  • First remove drift using Savitzky-Golay filter,

  • then apply gaussian smoothing apply fgrad.

‘sgsmooth_diff’:

  • First smooth the input signal x with Savitzky-Golay filter then apply

  • then apply gaussian smoothing (unnecessary, set gauss_window =0 to avoid) then apply fgrad

‘gauss_diff’:

  • First smooth the input signal x using gaussian smoothing

  • then apply fgrad

‘npdiff’:

  • npdiff uses numpy’s np.diff, which computes x[n+1] - x[n]

  • for compleness, npdiff is included.

Parameters:
x: 1d-array signal
method: method to compute derivative, one of the above
(sg_window,sg_polyorder,gauss_window,gauss_itr): Savitzky-Golay filter, Gaussian smoothing using Forward-Backward-Convolution (ConvFB)
Returns:
dx: derivative of signal

See also

filter_smooth_sGolay, filter_smooth_gauss, filter_with_kernel

Notes

  • Using fdiff and fgrad results in same output.

  • for noisy signal, applying smoothing first is always recommonded, (see example below)

References

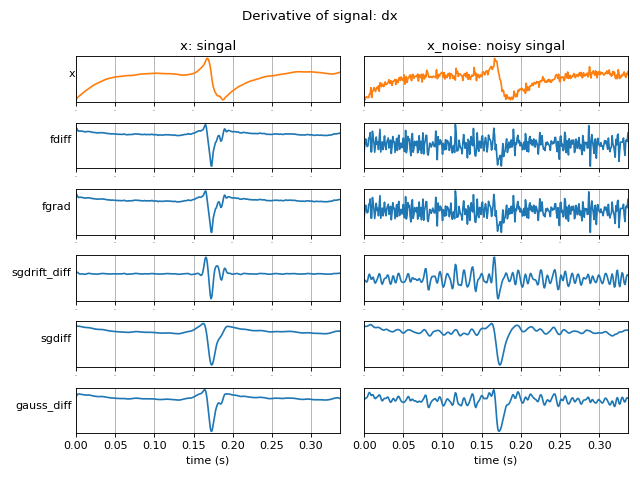
Examples

#sp.signal_diff
import numpy as np
import matplotlib.pyplot as plt
import spkit as sp
x, fs = sp.data.optical_sample(sample=2)
x = x[int(0.023*fs):int(0.36*fs)]
x = x - x.mean()
x_noise = sp.add_noise(x,snr_db=10)
t = np.arange(len(x))/fs

methods = ['fdiff','fgrad','sgdrift_diff','sgdiff','gauss_diff']
DX1 = [sp.signal_diff(x.copy(),method=method,sg_window=11,gauss_window=11) for method in methods]
DX2 = [sp.signal_diff(x_noise.copy(),method=method,sg_window=11,gauss_window=11) for method in methods]

figsize = (8,6)
K = len(DX1)

plt.figure(figsize=figsize)
plt.subplot(K+1,2,1)
plt.plot(t,x,'C1')
plt.xlim([t[0],t[-1]])
plt.ylabel(f'x',rotation=0)
plt.yticks([])
plt.xticks(fontsize=0)
plt.grid()
plt.title(f'x: singal')

plt.subplot(K+1,2,2)
plt.plot(t,x_noise,'C1')
plt.xlim([t[0],t[-1]])
#plt.ylabel(f'x')
plt.yticks([])
plt.xticks(fontsize=0)
plt.grid()
plt.title(f'x_noise: noisy singal')

for i in range(K):
    plt.subplot(K+1,2,i*2+3)
    plt.plot(t[:len(DX1[i])],DX1[i],color='C0')
    plt.xlim([t[0],t[-1]])
    plt.grid()
    plt.yticks([]) 
    #plt.xticks(labels='')
    plt.ylabel(methods[i],rotation=0, ha='right')
    if i==K-1:
        plt.xlabel('time (s)')
    else:
        plt.xticks(fontsize=0)

    plt.subplot(K+1,2,i*2+4)
    plt.plot(t[:len(DX2[i])],DX2[i],color='C0')
    plt.xlim([t[0],t[-1]])
    plt.grid()
    #if i<K-1:plt.xticks([])
    plt.yticks([])
    #plt.ylabel(f'$N={N[i]}$')
    #plt.legend(frameon=False,bbox_to_anchor=(1,1))
    if i==K-1:
        plt.xlabel('time (s)')
    else:
        plt.xticks(fontsize=0)

plt.suptitle('Derivative of signal: dx')
plt.subplots_adjust(hspace=0,wspace=0.05)
plt.tight_layout()
plt.show()
../../_images/spkit-signal_diff-1.png