spkit.bin_width¶
- spkit.bin_width(x, method='fd')¶
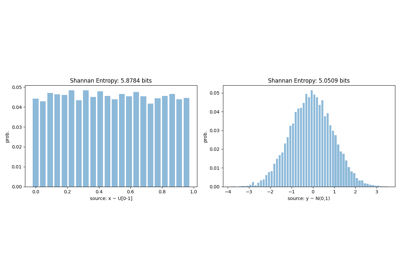
Compute bin width for histogram, using different methods
Compute bin width using different methods
- ‘fd’ (Freedman Diaconis Estimator)
Robust (resilient to outliers) estimator that takes into account data variability and data size.
- ‘doane’
An improved version of Sturges’ estimator that works better with non-normal datasets.
- ‘scott’
Less robust estimator that that takes into account data variability and data size.
- ‘stone’
- Estimator based on leave-one-out cross-validation estimate of the integrated squared error.
Can be regarded as a generalization of Scott’s rule.
- ‘rice’
- Estimator does not take variability into account, only data size.
Commonly overestimates number of bins required.
- ‘sturges’
Only accounts for data size. Only optimal for gaussian data and underestimates number of bins for large non-gaussian datasets.
- ‘sqrt’
Square root (of data size) estimator, used by Excel and other programs for its speed and simplicity.
- Parameters:
- x1d-array or (n-d array)
- methodmethod to compute bin width and number of bins
- Returns:
- bwbin width
- knumber of bins
See also
hist_plot# Histogram plot with optimal number of bins
References
wikipedia
Examples
>>> import numpy as np >>> import spkit as sp >>> np.random.seed(1) >>> t = np.linspace(0,2,200) >>> x1 = np.cos(2*np.pi*1*t) + 0.01*np.random.randn(len(t)) # less noisy >>> x2 = np.cos(2*np.pi*1*t) + 0.9*np.random.randn(len(t)) # very noisy >>> bw1, k1 = sp.bin_width(x1, method='fd') >>> bw2, k2 = sp.bin_width(x2, method='fd') >>> print(r'Optimal: bin-width of x1 = ',bw1,'\t Number of bins = ',k1) >>> print(r'Optimal: bin-width of x2 = ',bw2,'\t Number of bins = ',k2)