spkit.gaussian_kernel

spkit.gaussian_kernel(window_length, sigma_scale=2.7, sigma=None)

Gaussian Kernel

Gaussian Kernel

Generating Gaussian kernel of given window length and sigma.

sigma = window_length / 6

Parameters:

window_length: int, length of window

sigma_scale: float, to control the width and spread of gaussian curve

Returns:

ker: gaussian kernel of given window

See also

friedrichs_mollifier_kernel

Kurt Otto Friedrichs kernel

Examples

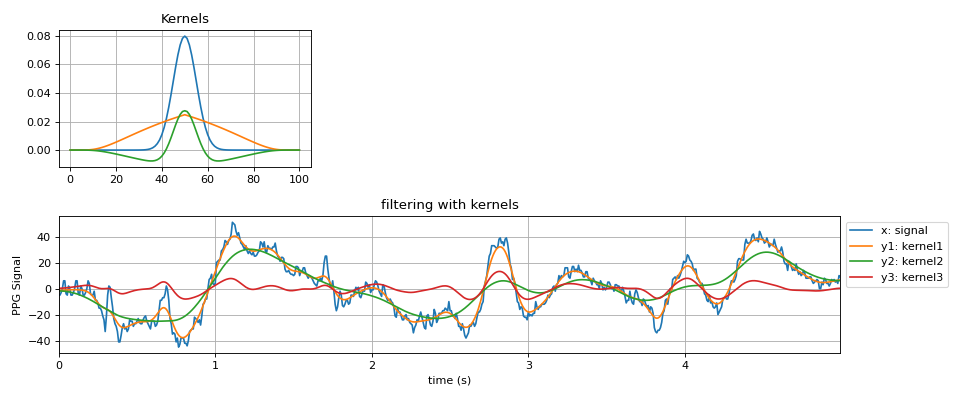
#sp.gaussian_kernel
import numpy as np
import matplotlib.pyplot as plt
import spkit as sp
x,fs = sp.data.ppg_sample(sample=1)
x = x[:int(fs*5)]
x = x - x.mean()
t = np.arange(len(x))/fs
kernel1 = sp.gaussian_kernel(window_length=101,sigma_scale=10)
kernel2 = sp.friedrichs_mollifier_kernel(window_size=101,s=1,p=1)
kernel3 = (kernel1 - kernel2)/2
y1 = sp.filter_with_kernel(x.copy(),kernel=kernel1)
y2 = sp.filter_with_kernel(x.copy(),kernel=kernel2)
y3 = sp.filter_with_kernel(x.copy(),kernel=kernel3)
plt.figure(figsize=(12,5))
plt.subplot(212)
plt.plot(t,x,label='x: signal')
plt.plot(t,y1,label='y1: kernel1')
plt.plot(t,y2,label='y2: kernel2')
plt.plot(t,y3,label='y3: kernel3')
plt.xlim([t[0],t[-1]])
plt.xlabel('time (s)')
plt.ylabel('PPG Signal')
plt.grid()
plt.legend(bbox_to_anchor=(1,1))
plt.title('filtering with kernels')
plt.subplot(231)
plt.plot(kernel1,label='kernel1')
plt.plot(kernel2,label='kernel2')
plt.plot(kernel3,label='kernel3')
plt.title('Kernels')
plt.grid()
plt.tight_layout()
plt.show()