spkit.Mu_law

spkit.Mu_law(x, Mu=255, companding=True)

μ-Law for companding and expanding (Non-linear mapping)

μ-Law is one of the ways to map gaussian, or laplacian distribuated signal to uniformly distributed one - for companding - smaller amplitude values are stretched (since they have high-probabilty)

and large amplitutde values are compressed (since they have low probabiltity)

  • for expending - it reverts the mapping

for -1 ≤ x ≤ 1

Companding:

\[y(n) = sign(x)* \frac{log(1 + μ|x|)}{log(1 + μ)}\]

expanding:

\[y(n) = sign(x)* \frac{((1 + μ)**|x| - 1)}{μ}\]

  • An alternative to A-Law

  • The μ-law algorithm provides a slightly larger dynamic range than the A-law at the cost of worse proportional distortions for small signals.

Parameters:
x1d (or nd) array

  • array of signal, must be -1 ≤ x ≤ 1

Muscalar (0≤Mu)

  • factor for companding-expanding mapping

  • ~0: identity function, higher value of Mu will stretch and compress more

  • use 1e-5 for Mu=0 to avoid ‘zero-division’ error

companding: bool, default=True

  • if True, companding is applied, else expanding

Returns:
y: mapped output of same shape as x

See also

A_law

A-Law for companding and expanding

References

Examples

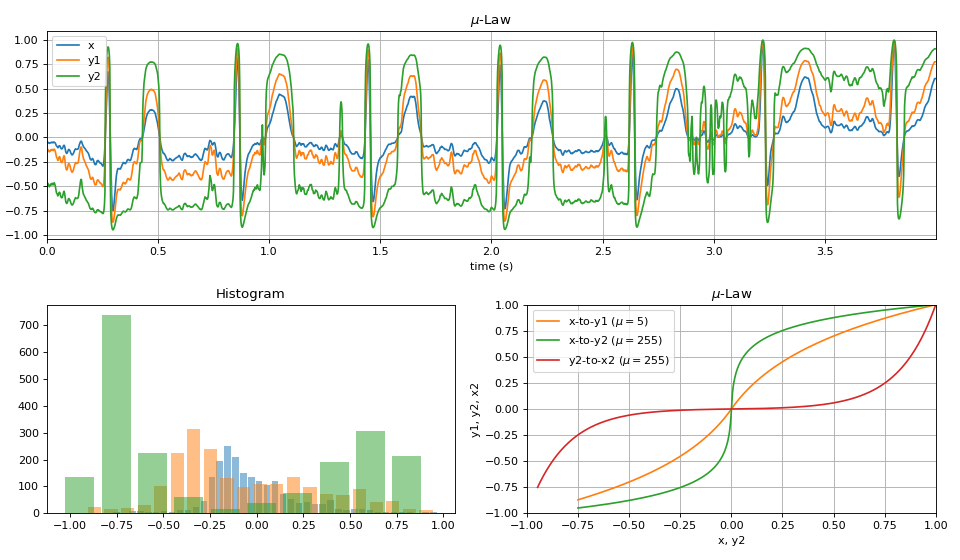
#sp.Mu_law
import numpy as np
import matplotlib.pyplot as plt
import spkit as sp
x,fs,_ = sp.data.ecg_sample_12leads(sample=3)
x = x[1000:3000,0]
x = x/(np.abs(x).max()*1.01)
x = x - np.mean(x)
x = x/(np.abs(x).max()*1.01)
t = np.arange(len(x))/fs
y1 = sp.Mu_law(x.copy(),Mu=5,companding=True)
y2 = sp.Mu_law(x.copy(),Mu=255,companding=True)
x2 = sp.Mu_law(y2.copy(),Mu=255,companding=False)
plt.figure(figsize=(12,7))
plt.subplot(211)
plt.plot(t,x,label=f'x')
plt.plot(t,y1,label=f'y1')
plt.plot(t,y2,label=f'y2')
plt.xlim([t[0],t[-1]])
plt.xlabel('time (s)')
plt.legend()
plt.title('$\mu$-Law')
plt.grid()
plt.subplot(223)
sp.hist_plot(x)
sp.hist_plot(y1)
sp.hist_plot(y2)
plt.title('Histogram')
plt.subplot(224)
idx = np.argsort(x)
plt.plot(x[idx],y1[idx],color='C1',label='x-to-y1 ($\mu=5$)')
plt.plot(x[idx],y2[idx],color='C2',label='x-to-y2 ($\mu=255$)')
plt.plot(y2[idx],x[idx],color='C3',label='y2-to-x2 ($\mu=255$)')
plt.xlim([-1,1])
plt.ylim([-1,1])
plt.xlabel('x, y2')
plt.ylabel('y1, y2, x2')
plt.title(r'$\mu$-Law')
plt.grid()
plt.legend()
plt.tight_layout()
plt.show()
../../_images/spkit-Mu_law-1.png