spkit.ICA

class spkit.ICA(n_components=None, max_pca_components=None, n_pca_components=None, random_state=None, method='fastica', fit_params=None, max_iter=200)

Independent Component Analysis

Signal decomposition using Independent Component Analysis (ICA), very usefule for EEG signal decompositions Including InfoMax, Extendent InfoMax and Picard methods, default as FastICA as usual

\[ \begin{align}\begin{aligned}S = A*X\\X = W*S\end{aligned}\end{align} \]
where:

  • X : input data shape (nf,ns), nf- number of features or number of channels, ns- number of samples

  • S : decomposed data (n,ns) n - number of components choosen, default n=nf

  • A : Transform matirx (n,n)

  • W : inverse transform matrix (n,n)

Python implementation of the ICA algorithms: FastICA including, infomax, extendented infomax and picard.

Parameters:
n_componentsint, None

  • The number of components used for ICA decomposition. it must be smaller than ‘max_pca_components’.

  • If None, all PCA components will be used default None, set to max number of components

max_pca_componentsint, None

  • The number of components used for PCA decomposition. If None, no dimensionality reduction will be applied and max_pca_components will equal the number of channels (number of features) supplied for decomposing data.

n_pca_components: int, float

  • The number of PCA components used after ICA recomposition.

random_state: None, int,

  • instance of np.random.RandomState

method{‘fastica’, ‘infomax’, ‘extended-infomax’, ‘picard’}

The ICA method to use. Defaults to ‘fastica’. For reference, see [1]_, [2]_, [3]_ and [4]_.

fit_paramsdict, None

Additional parameters passed to the ICA estimator as specified by method.

max_iterint

Maximum number of iterations during fit.

Attributes:
Estimated Values
* pca_mean_

  • mean substacted from data before computing PCA

* pca_components_

  • PCA transform matrix

* pca_explained_variance_

  • variance of Principle components

* unmixing_matrix_

  • ICA unmixing matrix A

* mixing_matrix_

  • ICA mixing matrix W

* whitener_

  • Standard deviaation of data before applying ICA

* n_components
* max_pca_components
* n_pca_components
* random_state
* fit_params

Notes

fit(self, X, normalize=False):

Fitting to data matrix X, X ndarray (nf,ns)

transform(self, Xdata):

Decompose Xdata into Independent Components return Xd (ndarray)

get_tMatrix(self):

Get Tranformation matrix return A (n,n)

get_sMatrix(self):

Get Inverse Transform matrix return W (n,n)

whitening(self, X):

To normlize the standard deviation of entire data (not the usual normailization)

References

  • [1] Hyvärinen, A., 1999. Fast and robust fixed-point algorithms for

    independent component analysis. IEEE transactions on Neural Networks, 10(3), pp.626-634.

  • [2] Bell, A.J., Sejnowski, T.J., 1995. An information-maximization

    approach to blind separation and blind deconvolution. Neural computation, 7(6), pp.1129-1159.

  • [3] Lee, T.W., Girolami, M., Sejnowski, T.J., 1999. Independent

    component analysis using an extended infomax algorithm for mixed subgaussian and supergaussian sources. Neural computation, 11(2), pp.417-441.

  • [4] Ablin, P., Cardoso, J.F., Gramfort, A., 2017. Faster Independent

    Component Analysis by preconditioning with Hessian approximations. arXiv:1706.08171

Examples

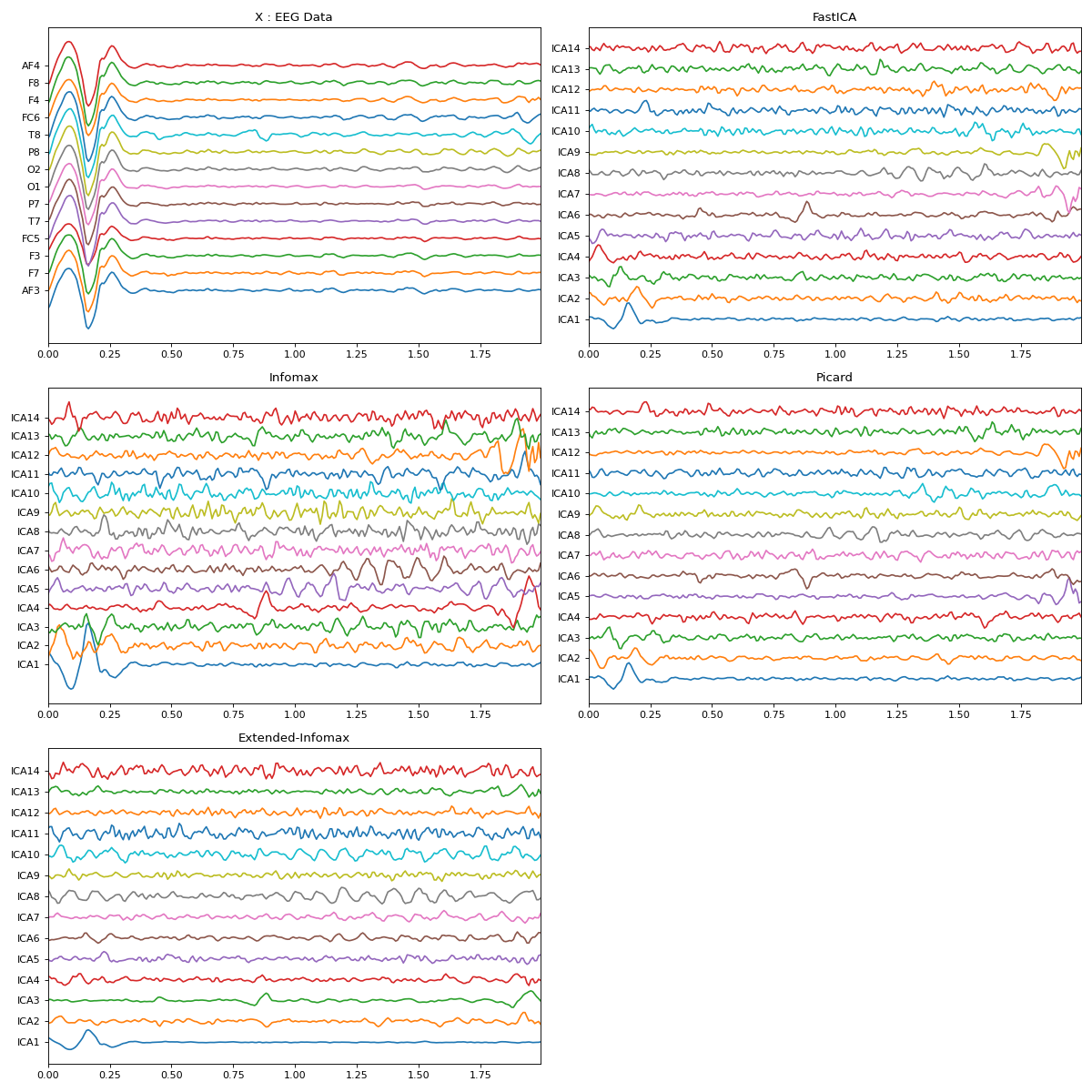
import numpy as np
import matplotlib.pyplot as plt
import spkit as sp
X,fs, ch_names = sp.data.eeg_sample_14ch()
Xf = sp.filterDC_sGolay(X, window_length=fs//3+1)

x = Xf[128*10:128*12,:]
t = np.arange(x.shape[0])/128.0

myICA = sp.ICA(n_components=14,method='fastica')
myICA.fit(x.T)
s1 = myICA.transform(x.T)

myICA = sp.ICA(n_components=14,method='infomax')
myICA.fit(x.T)
s2 = myICA.transform(x.T)

myICA = sp.ICA(n_components=14,method='picard')
myICA.fit(x.T)
s3 = myICA.transform(x.T)

myICA = sp.ICA(n_components=14,method='extended-infomax')
myICA.fit(x.T)
s4 = myICA.transform(x.T)

methods = ('fastica', 'infomax', 'extended-infomax', 'picard')
icap = ['ICA'+str(i) for i in range(1,15)]

plt.figure(figsize=(15,15))
plt.subplot(321)
plt.plot(t,x+np.arange(-7,7)*200)
plt.xlim([t[0],t[-1]])
plt.yticks(np.arange(-7,7)*200,ch_names)
plt.title('X : EEG Data')

plt.subplot(322)
plt.plot(t,s1.T+np.arange(-7,7)*700)
plt.xlim([t[0],t[-1]])
plt.yticks(np.arange(-7,7)*700,icap)
plt.title('FastICA')

plt.subplot(323)
plt.plot(t,s2.T+np.arange(-7,7)*700)
plt.xlim([t[0],t[-1]])
plt.yticks(np.arange(-7,7)*700,icap)
plt.title('Infomax')

plt.subplot(324)
plt.plot(t,s3.T+np.arange(-7,7)*700)
plt.xlim([t[0],t[-1]])
plt.yticks(np.arange(-7,7)*700,icap)
plt.title('Picard')

plt.subplot(325)
plt.plot(t,s4.T+np.arange(-7,7)*700)
plt.xlim([t[0],t[-1]])
plt.yticks(np.arange(-7,7)*700,icap)
plt.title('Extended-Infomax')
plt.tight_layout()
plt.show()
../../_images/spkit-ICA-1.png

Methods

fit(X[, normalize])

Fitting to data matrix X, X ndarray (nf,ns)

get_sMatrix()

Get Inverse Transform matrix

get_tMatrix()

Get Tranformation matrix

transform(Xdata)

Decompose Xdata into Independent Components

whitening(X)

Whitening of matrix
fit(X, normalize=False)

Fitting to data matrix X, X ndarray (nf,ns)

Run the ICA decomposition on X.

Parameters:
X = array like:

  • Shape (nf,ns) or (nCh, nSamples)

get_sMatrix()

Get Inverse Transform matrix

Get Final ICA weight matrix.

Returns:
Matrixarray, shape (n_channels, n_components)

The ICA weights (maps).

get_tMatrix()

Get Tranformation matrix

transform(Xdata)

Decompose Xdata into Independent Components

Compute sources from data (operates inplace).

whitening(X)

Whitening of matrix

Examples using spkit.ICA

Independed Principle Component analysis

Independed Principle Component analysis