spkit.geometry.get_adjacency_matrix_dist

spkit.geometry.get_adjacency_matrix_dist(V, dist=5, remove_self_con=True, ignore_matrix=False)

Create Adjacency Matrix based on Euclidean distance

Parameters:

V: array (n,d),

• vertices, n-points in d-dimentional space

dist: float, distance

Returns:

AdjM: (n,n)

• Binary Adjacency Matrix

node2C: dict,

• Dictionary of node to connection list node2C[node_a] = list_of_nodes_connected_to_node_a

Examples

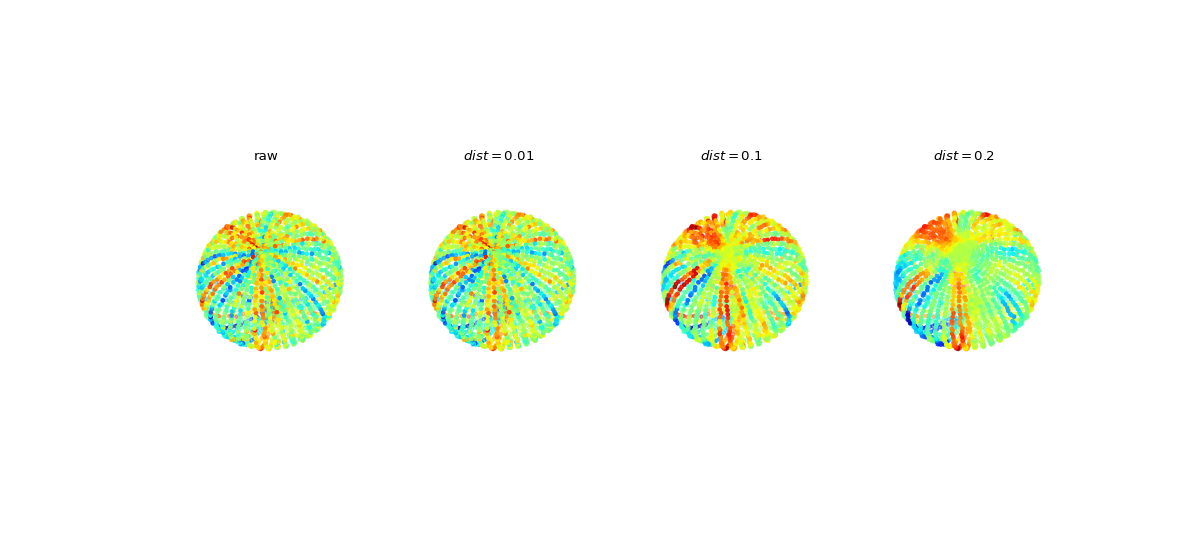
#sp.geometry.get_adjacency_matrix_dist
import numpy as np
import matplotlib.pyplot as plt
import spkit as sp

V = sp.geometry.get_ellipsoid(n1=50, n2=50, rx=1, ry=2, rz=1,)
V += 0.01*np.random.randn(V.shape[0],V.shape[1])

X = sp.create_signal_1d(V.shape[0],bipolar=False,sg_winlen=21,sg_polyorder=2,seed=1)
X += 0.1*np.random.randn(X.shape[0]) 

AdjM1, _  = sp.geometry.get_adjacency_matrix_dist(V, dist=0.01)
AdjM2, _  = sp.geometry.get_adjacency_matrix_dist(V, dist=0.1)
AdjM3, _  = sp.geometry.get_adjacency_matrix_dist(V, dist=0.2)

Y1 = sp.graph_filter_adj(X,AdjM1,ftype='mean',exclude_self=False)
Y2 = sp.graph_filter_adj(X,AdjM2,ftype='mean',exclude_self=False)
Y3 = sp.graph_filter_adj(X,AdjM3,ftype='mean',exclude_self=False)

fig, ax = plt.subplots(1,4,subplot_kw={"projection": "3d"},figsize=(15,7))

Ys =[X, Y1, Y2, Y3]
TITLEs = ['raw', r'$dist=0.01$',r'$dist=0.1$', r'$dist=0.2$']
for i in range(4):
    ax[i].scatter3D(V[:,0], V[:,1], V[:,2], c=Ys[i], cmap='jet',s=10)
    ax[i].axis('off')
    ax[i].view_init(elev=60, azim=45, roll=15)
    ax[i].set_xlim([-1,1])
    ax[i].set_ylim([-2,2])
    ax[i].set_zlim([-1,1])
    ax[i].set_title(TITLEs[i])

plt.subplots_adjust(hspace=0,wspace=0)
plt.show()