spkit.elbow_knee_point

spkit.elbow_knee_point(x, dx=None, plot=False, show=False, show_lines=False, lw=1)

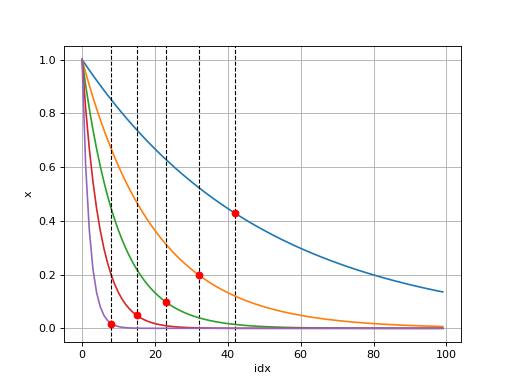
Finding Elbow-knee point of a curve

The algorithm computes the perpendicular distance between each curve point to base vector. where base vector is line between first and last point of curve.

\[ \begin{align}\begin{aligned}dist = |p - (p \cdot b') b'|\\b' = b/|b|\\idx = argmax(dist)\end{aligned}\end{align} \]
Parameters:
x: 1d array

  • input curve,

dx: None, or 1d-array, default=None

  • if None, curve points are assumed to be evenly spaced.

  • if not None, then dx is the points for x is computed on.

plot: bool, False

  • if True, plot the curve, and knee point

show_dist: bool, default=False,

  • if True, show distance computed to use for knee point

show: bool, default=False

  • if True, plt.show() is excecuted, else not, to be used for addtional plt commands to be affective

Returns:
idx: int,

  • index of the knee point in the curve

Notes

  • Knee point is not very accurate if curve x is noisy. Apply this algorithm with smooth curve x

References

Examples

import numpy as np
import matplotlib.pyplot as plt
import spkit as sp
t = np.arange(100)/99
x = np.exp(-2*t)
idx = sp.elbow_knee_point(x,plot=True,show_lines=False)
x = np.exp(-5*t)
idx = sp.elbow_knee_point(x,plot=True,show_lines=False)
x = np.exp(-10*t)
idx = sp.elbow_knee_point(x,plot=True,show_lines=False)
x = np.exp(-20*t)
idx = sp.elbow_knee_point(x,plot=True,show_lines=False)
x = np.exp(-50*t)
idx = sp.elbow_knee_point(x,plot=True,show_lines=False)
plt.grid()
plt.show()
../../_images/spkit-elbow_knee_point-1.png