spkit.SVD

spkit.SVD(X, full=True)

Singular Value Decomposition,

returns full matrixes without truncating zeros from S matrix

Parameters:
X - MxN, array
Returns:
return (if full True)

  • U - MxM

  • S - MxN

  • V - NxN

Examples

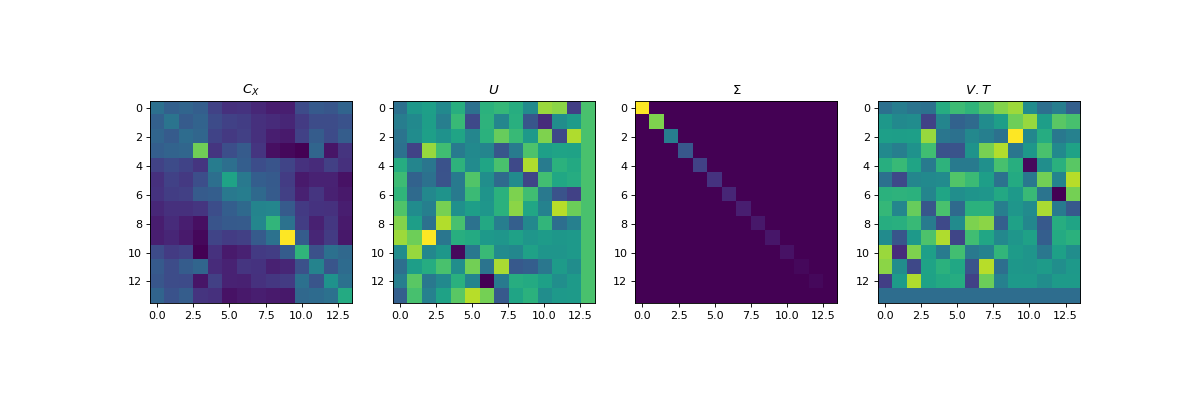
#sp.SVD
import numpy as np
import matplotlib.pyplot as plt
import spkit as sp
X,fs, ch_names = sp.data.eeg_sample_14ch()
Xf = sp.filterDC_sGolay(X, window_length=fs//3+1)
Xf = Xf-Xf.mean(1)[:,None] 
print(Xf.shape)
CX = np.dot(Xf.T,Xf)/(Xf.shape[0]-1)
print(CX.shape)
U,S,V = sp.SVD(CX)
print(U.shape, S.shape, V.shape)
plt.figure(figsize=(15,5))
plt.subplot(141)
plt.imshow(CX)
plt.title(r'$C_X$')
plt.subplot(142)
plt.imshow(U)
plt.title(r'$U$')
plt.subplot(143)
plt.imshow(S)
plt.title(r'$\Sigma$')
plt.subplot(144)
plt.imshow(V.T)
plt.title(r'$V.T$')
plt.show()
../../_images/spkit-SVD-1_00_00.png 
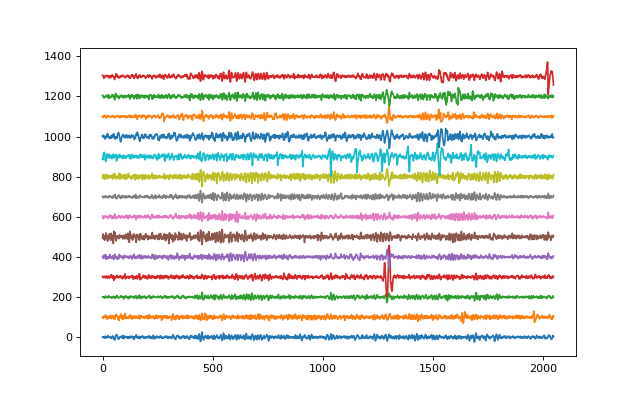
plt.figure(figsize=(8,5))
plt.plot(Xf+ np.arange(14)*100)
plt.show()
../../_images/spkit-SVD-1_01_00.png 
print('Validate : Cx = U x S x V.T')
np.allclose(np.dot(np.dot(U, S), V.T),CX)